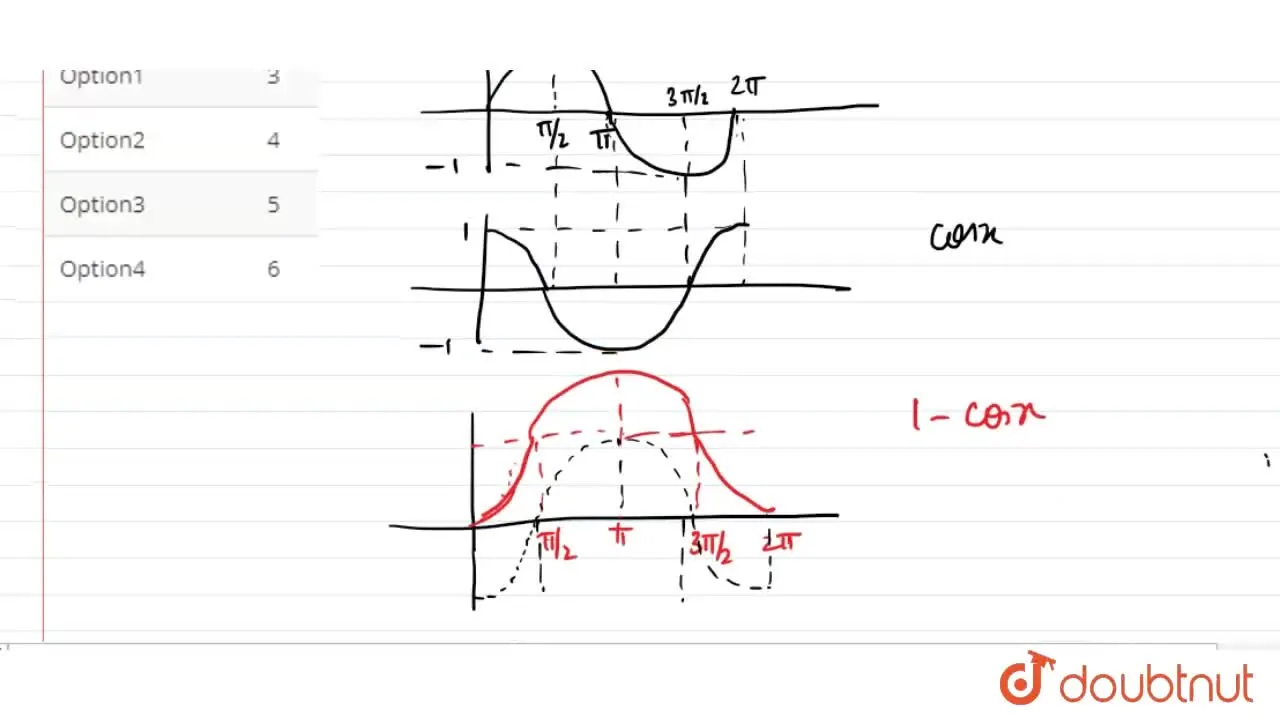
In (0,2π), the total number of points where f(x)=max.{sin x, cos x, 1 - cos x} is not differentiable , are equal to
3
4
5
6
The correct Answer is:A
Step by step video & image solution for In (0, 2pi), the total number of points where f(x)=max.{sin x, cos x, 1 - cos x} is not differentiable , are equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Number of points where f(x)=max{2−|x|,min{x2−1}} is not differentiable.is
View SolutionThe number of points where f(x) = max {|sin x| , | cos x|} , x∈(−2π,2π) is not differentiable is ______
View SolutionFind the number of points where the function f(x)=max|tanx|,cos|x|) is non-differentiable in the interval (−π,π).
View SolutionThe total number of points where the function f:R→R given by f(x)=sinx1+|x| is not-differentiable
View SolutionLet f(x)=max{4,1+x2,x2−1}∀x∈R Total numbner of points , where f(x) is non -differentiable , is equal to
View SolutionLet f(x)= max{4,1+x2,x2−1}∀x∈R. Total number of points, where f (x) is non-differentiable, is equal to
View SolutionThe total number of solution of sin4x+cos4x=sinxcosx in [0,2π]
View SolutionLet g(x)=∣∣4x3−x∣∣cos(πx) then number of points where g(x) is non-differentiable in (−∞,∞) ,is equal to
View SolutionIf the number of points of non differentiable of f(x)=max{sinx,cosx,0} in (0,2nπ) is Pn then find the value P
View SolutionIf f(x)=max{sinx,sin−1(cosx)}, then
View Solution