Prove that the equation 2sinx=|x|+a has no solution for a∈(3√3−π3,∞).
Video Solution
Text Solution
sinx=12|x|+a2
Draw the graphs of y=2sinxandy=|x|.
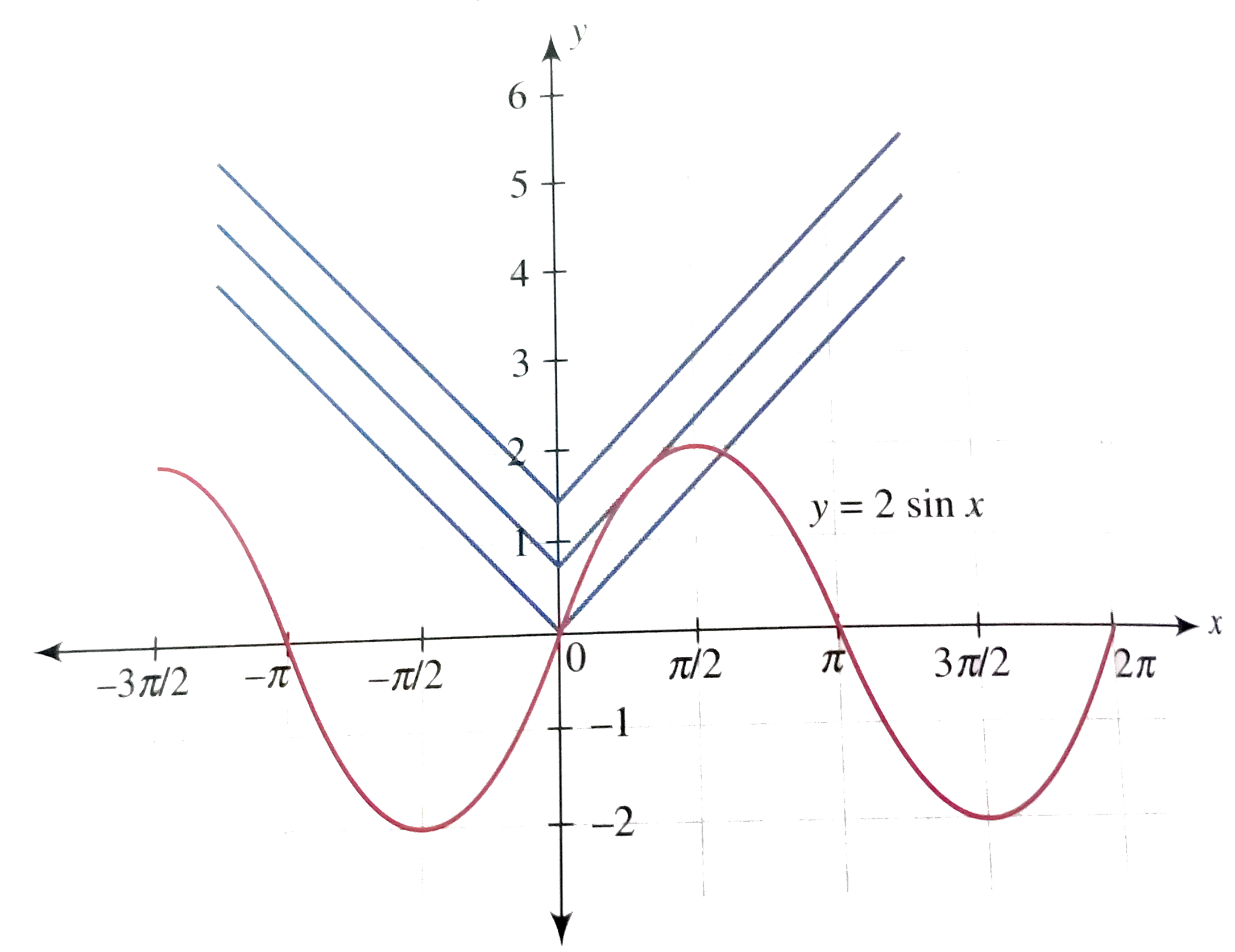
The equation 2sinx=|x|+a will have a solution so long as the line y=|x|+a intersects or at least touches the curve y=2sinx. When the graphs touch, we have
dydx=2cosx=1,⇒x=π3
Hence for no solution,
π3+a>2sinπ3
⇒a>3√3−π3
|
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
Similar Questions
Knowledge Check
The equation |sinx|=sinx+3has in[0,2π]
Ano rootBonly one rootCtwo rootsDmore than two rootsFind the principal solution of the equation sinx=√32.
A(π3,2π3)B(π6,5π6)C(3π5,−π6)DNone of theseThe equation √3⋅sinx+cosx=4 has
Aonly one solutionBtwo solutionsCinfinitely many solutionsDno solution
Prove that the equation 3(sinx+cosx)−2(sin3x+cos3x)=8, has no solution.
View SolutionThe equation √3sinx+cosx=4 has
View SolutionFind the principal solution of the equation sinx=√32.
View SolutionFind number of solution of the equation 2sinx+5sin2x+8sin3x+...∞=1 for x∈[0,2π].
View SolutionFor x∈(0,π) the equation sinx+2sin2x−sin3x=3 has
View Solution
