The number of solution of $2 cos x = | sin x |$ where $x \in [0.4 π]$ is/are

Video Solution

Text Solution

Verified by Experts

To find the number of solutions to the equation $2 cos x = | sin x |, 0 \leq x \leq 4 π$ , we need to find how many times the graphs of $y = 2 cos x and y = | sin x |$ intersect in $[0, 4 π]$ .
The graphs of $y = 2 cos x and y = | sin x |$ are plotted as ss

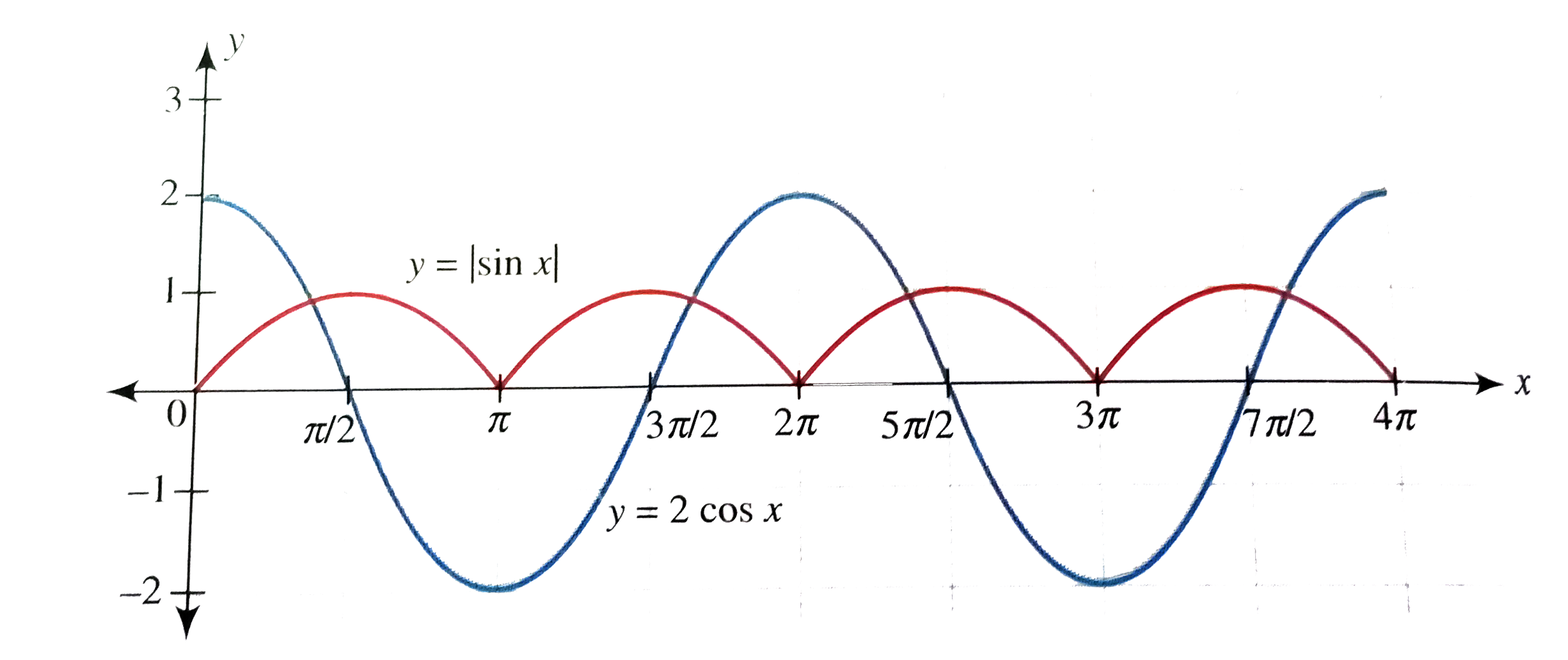
We find that the graphs intersect at four points. Hence the equation has four solutions.

Updated on:21/07/2023

|

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

The number of solution of $cos x = | 1 + sin x |, 0 \leq x \leq 3 π$ is
A2
B3
C4
D5
The number of solutions of $2 cos x = | sin x |, 0 \leq x \leq 4 π,$ is
A0
B2
C4
Dinfinite
The number of solutions of $| cos x | = sin x, 0 \leq x \leq 4 π$ is-
A8
B4
C2
DNone of the these

CENGAGE-GRAPHICAL TRANSFORMATIONS-Exercise

Home
Ask Doubt
Profile