Question

Solve $|x-1|-|x+3|<6$ graphically

Explanation

We have `|x-1|-|x+3|lt6`
or `|x-1|lt6+|x+3|`
Draw the graphs of `y=|x-1|andy=6+|x+3|`
`y=|x-1|` has vertex at (1,0),
For `y=6+|x+3|`, the graph of `y=|x|` shifts '3' units to the left horizaontally and then '6' units upaward vertically.
So the graphs of both function are as shown in the following figure.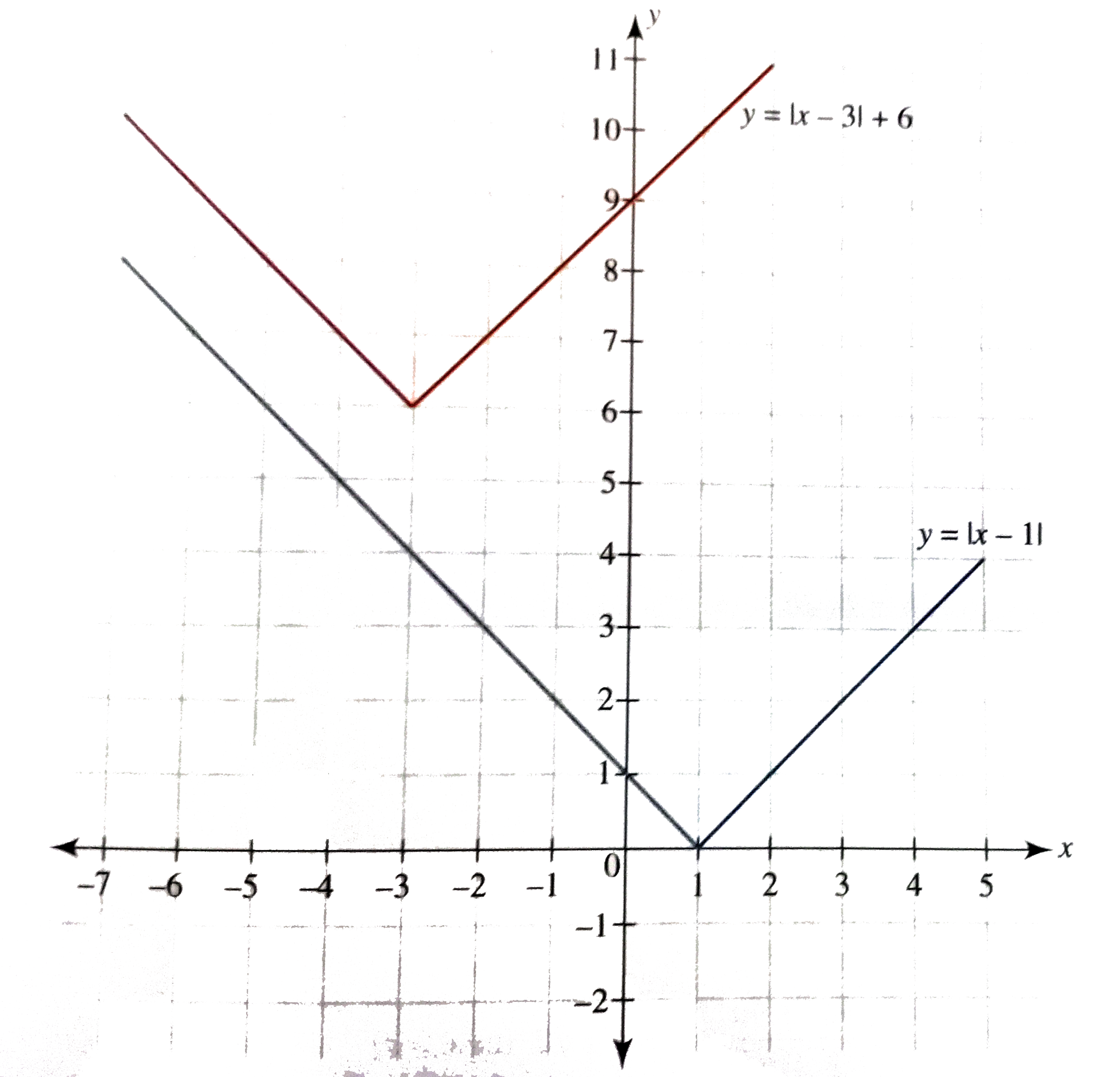
From the figure, the graph of `y=|x-1|` always lies below the graph of `y=6+|x+3|`. Hence solution is R.