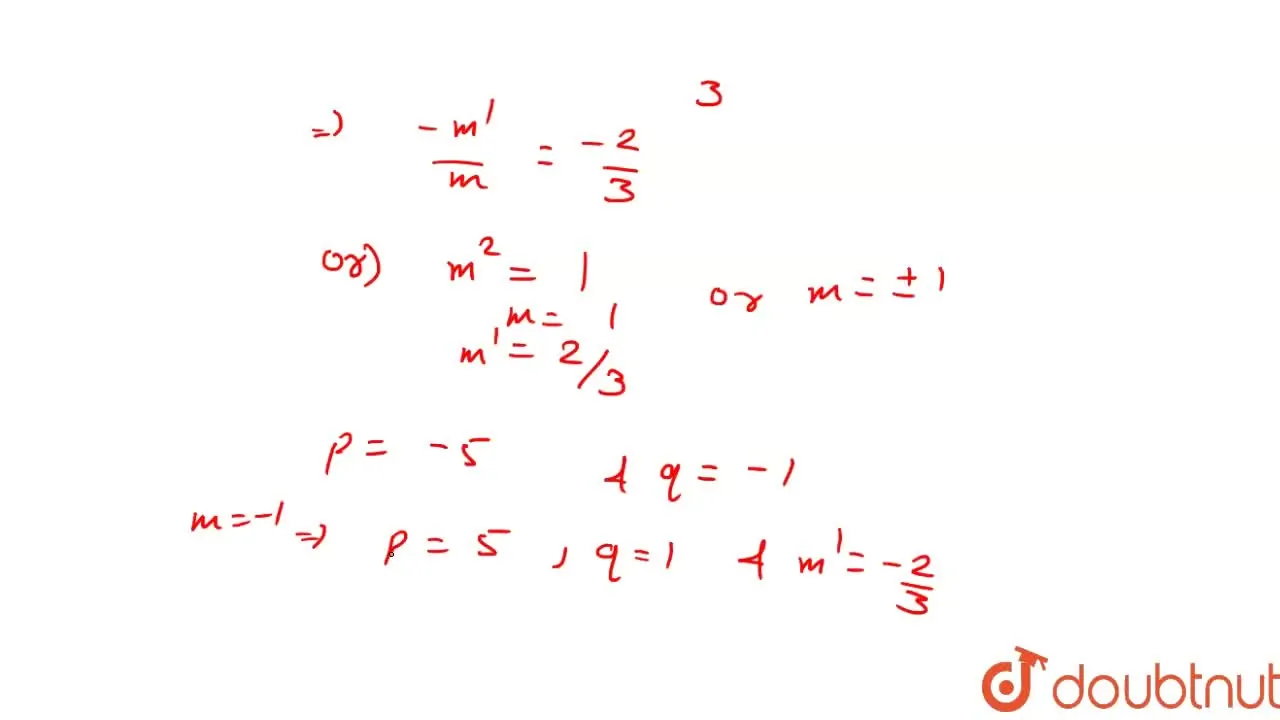If one of the lines given by the equation 2x2+pxy+3y2=0 coincide with one of those given by 2x2+qxy−3y2=0 and the other lines represented by them are perpendicular , then value of p+qis
6
-6
-7
7
The correct Answer is:1 ,2
Let 23x2+p3xy+y2=(y−mx)(y−m'x)
and 2−3x2+q−3xy+y2=(y+1mx)(y−m'x) then ,
m+m'=−p3,mm'=23 (1)
1m−m'=−q3,−m'm=−23 (2)
or m2=1orm=±1
If m=1,m'=2/3 and , so , p =-5,q=-1,m'=−2/3 and , so , p =5 , q =1.
Related Playlists
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Comprehension)6videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Single)23videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Question Bank21videos
PARABOLA
Similar Questions
If one of the lines given by the equation 2z2+axy+3y2=0 coincide with one of those given by 2x2+bxy−3y2=0 and the other lines represented by them be perpendicular, then
View SolutionIf one of the lines given by the equation 2x2+pxy+3y2=0 coincide with one of those given by 2x2+qxy−3y2=0 and the other lines represented by them are perpendicular, then (a)p=5 (b) p=−5 (c)q=−1 (d) q=1
View Solutionif one of the lines given by the equation ax2+2hxy+by2=0 coincides with one of the lines given by a'x2+2h'xy+b'y2=0 and the other lines representted by them be perpendicular , then .
ha'b'b'−a'=h'abb−a=12√(−aa'′).View SolutionIf one of the lines represented by the equation ax2+2hxy+by2=0 is coincident with one of the lines represented by a'x2+2h'xy+b'y2=0 , then
View SolutionIf the line 3x−2y=0 coincide with one of the lines given by ax2+2hxy+by2=0, then
View SolutionIf one of the two lines 6x2+xy−y2=0 coincides with one of the two lines 3x2−axy+y2=0 ten
View SolutionIf the line 4x−5y=0 coincide with one of the lines given by ax2+2hxy+by2=0, then
View SolutionIf the line 4x+5y=0 coincide with one of the lines given by ax2+2hxy+by2=0, then
View SolutionIf line 4x−3y=0 coincides with one of the lines ax2+2hxy+by2=0 then
View SolutionIf 2x+y=0 is one of the lines given by 3x2+kxy+2y2=0, then k=
View Solution