Question

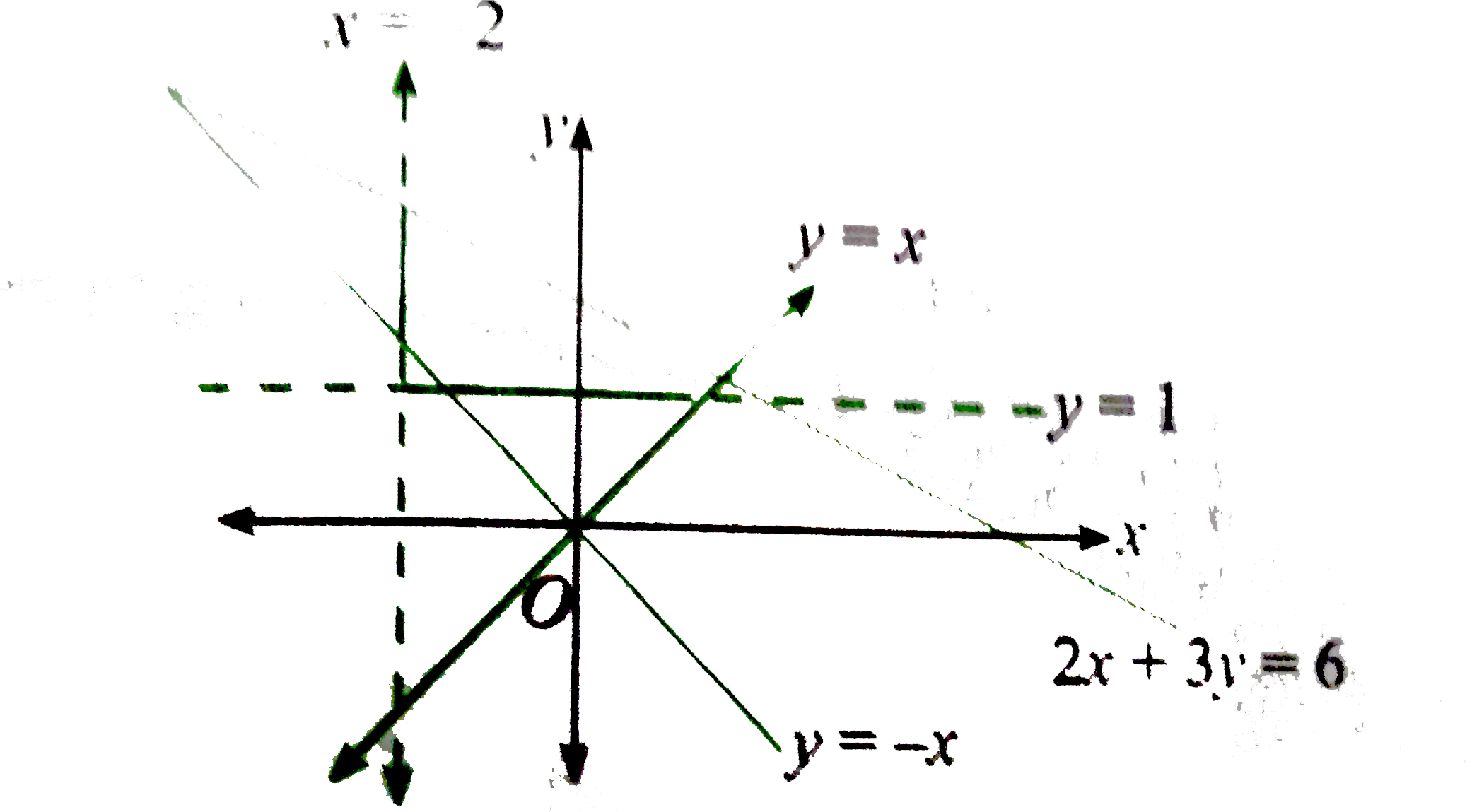
The combined equation of three sides of a triangle is $(x^2-y^2)(2x+3y-6)=0$
. If $(-2,a)$
is an interior point and $(b,1)$
is an exterior point of the triangle, then
$2<a<\frac{10}{3}$
(b)
$-2<a<\frac{10}{3}$

$-1<b<\frac{9}{2}$
(d) $-1<b<1$

Options

A. `2ltalt10//3`
B. `-2ltalt10//3`
C. `-1ltblt9//2`
D. `-1ltblt1`

Answer

1,4

Explanation

The separate equations of the sides are `x-y=0,x+y=0and 2x+3y-6=0` . The point (-2,a) moves on the line `x=-2` and the point (b,1) moves on the line `y=1` . From the figure , the y- coordinates of the points of intersection of `x=-2` with `y=-xand2x+3y=6` given the range of values of a . The x - coordinates of the points of intersection of `y=1` with `y=-xand y=x` give the range of values of b.