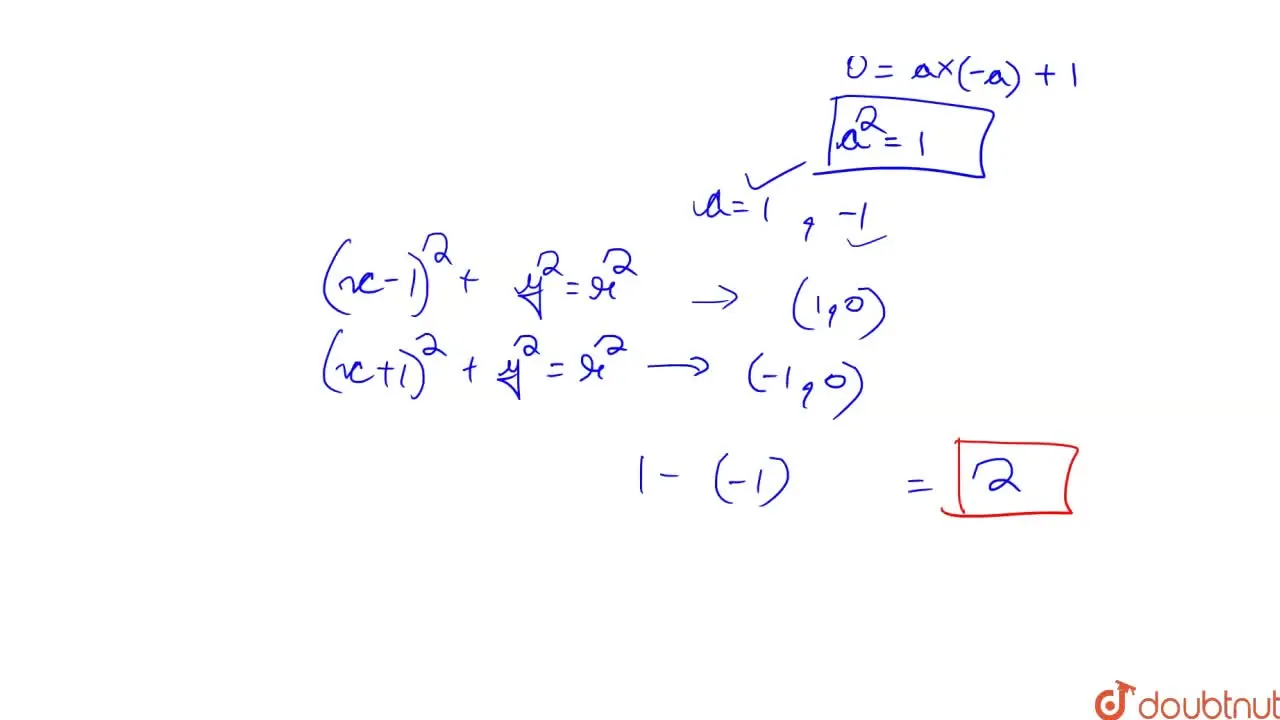Two circles with equal radii are intersecting at the points (0, 1) and (0,-1). The tangent at the point (0,1) to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is.
1
√2
2√2
2
The correct Answer is:D
Step by step video, text & image solution for Two circles with equal radii are intersecting at the points (0, 1) and (0,-1). The tangent at the point (0,1) to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 5 (Parabola)8videos
JEE 2019
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 6 (Ellipse)3videos
JEE 2019
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 2 (Straight Lines)8videos
JEE 2019
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank24videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - Question Bank30videos
LIMITS
Similar Questions
Two circles with equal radii are intersecting at the points (1,0) and (−1,0). Then tangent at the point (1,0) to one of the circles passes through the centre of the other circle.Then the distance between the centres of these circles is:
View SolutionThe angle between the two circles, each passing through the centre of the other is
View SolutionTwo circle intersect each other such that each circle passes through the centre of the other. If the distance between their centres is 12 , what is the radius of each circle?
View SolutionTwo circles of equal radii intersect each other such that one circle will pass through the centre of the other circle. The distance between the centre of two circles is equal to 6 cm. Find the length (in cm) of common chord.
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View SolutionIf we draw a tangents to a circle at a given point on it, when the centre of the circle is known, then the angle between the tangent and radius of the circle is
View SolutionA circle passes through (0,0) and (1,0) and touches the circle x2+y2=9 then the centre of circle is -
View SolutionThe equation of any circle passing through the points of intersection of the circle S=0 and the line L=0 is
View SolutionTwo circle touch each other externally at the point (0,k) and y-axis is the common tangent to these circles. Centres of these circle lie on the line
View SolutionIf a circle passes through (0,0),(4,0) and touches the circle x2+y2=36 then the centre of circle
View Solution