$(p \land ~ q) \land (~ p \land q)$ is

A

a contradiction

B

a tautology

C

either (1) or (2)

D

neither (1) nor (2)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

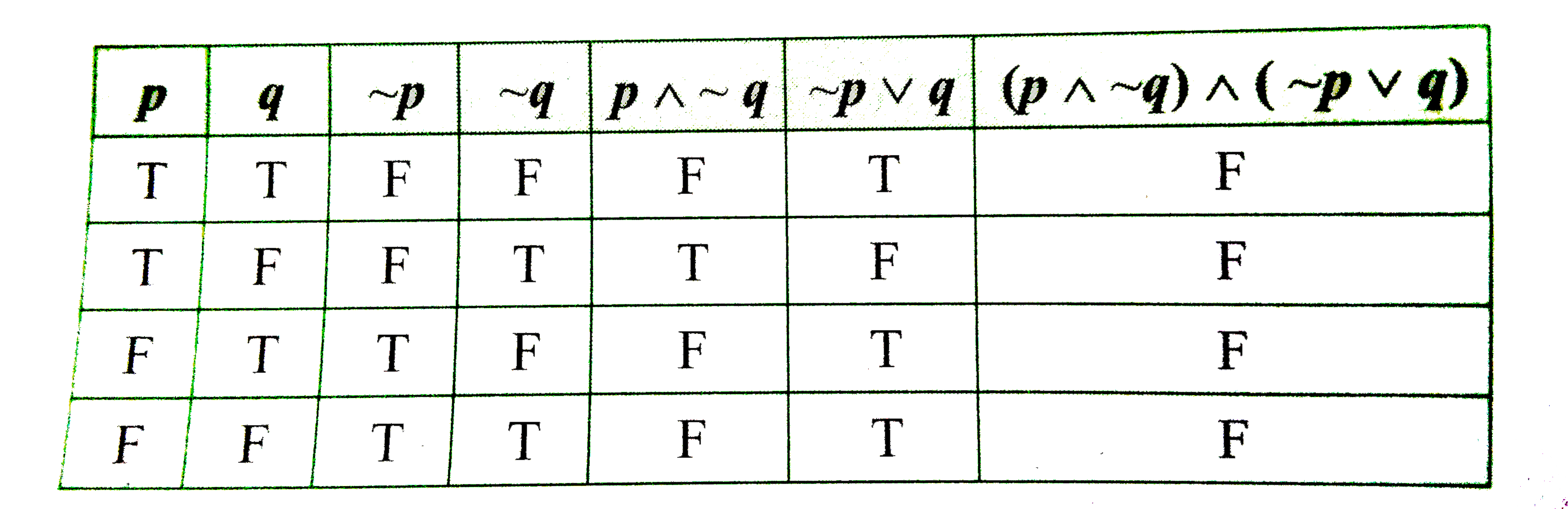
Clearly, $(p \land ~ q) \land (~ p \lor q)$ is a contradiction.

Updated on:21/07/2023

|

Class 12 MATHS MATHMETICAL REASONING

Topper's Solved these Questions

MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year
10 Videos
MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.2
5 Videos
LOGARITHM AND ITS PROPERTIESBOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year
5 Videos
MATRICESBOOK - CENGAGECHAPTER - MATRICESEXERCISE - Solved Examples And Exercises
165 Videos

Similar Questions

Knowledge Check

STATEMENT-1 : $(p \land ~ q) \land (~ p \land q)$
and
STATEMENT-2 : $(p \lor ~ q) \lor (~ p \land q)$
AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1
CStatement-1 is True, Statement-2 is False
DStatement-1 is False, Statement-2 is True
The simplified form of $(p \land q) \lor (p \land ~ q)$ is
Ap
Bq
C $p \land q$
D $p \lor q$
$(p \land ~ q) \land (~ p \lor q)$ is
Aa contradiction
Ba tautology
CEither (a) or (b)
DNeigher (a) nor (b)

CENGAGE-MATHMETICAL REASONING-Exercise (Single)

Home
Ask Doubt
Profile