A particle is moving along x-axis under the action of a force F, which varies with its position (x)asf∝1√x.Find the variation of power due to this force with x.
x13
x18
x12
x14
The correct Answer is:(2)
F∞x−14⇒a∞x−14
a=kx−14
dvdt=vdvdx=kx−14
∫vdv=k∫x−14dx
v22=kx3434
v2∞x34⇒v∞x38
∴P=Fv⇒P∞x38x14
P∞x18
Topper's Solved these Questions
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -II (H.W)
Explore 75 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -III
Explore 54 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -1 (H.W)
Explore 60 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-IV
Explore 56 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
Similar Questions
A particle is moving along x-axis under the action of force, F which varies with its position as F∝14√x. Find the variation of power due to this fore with x.
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) varsus position (x) graph is given, then
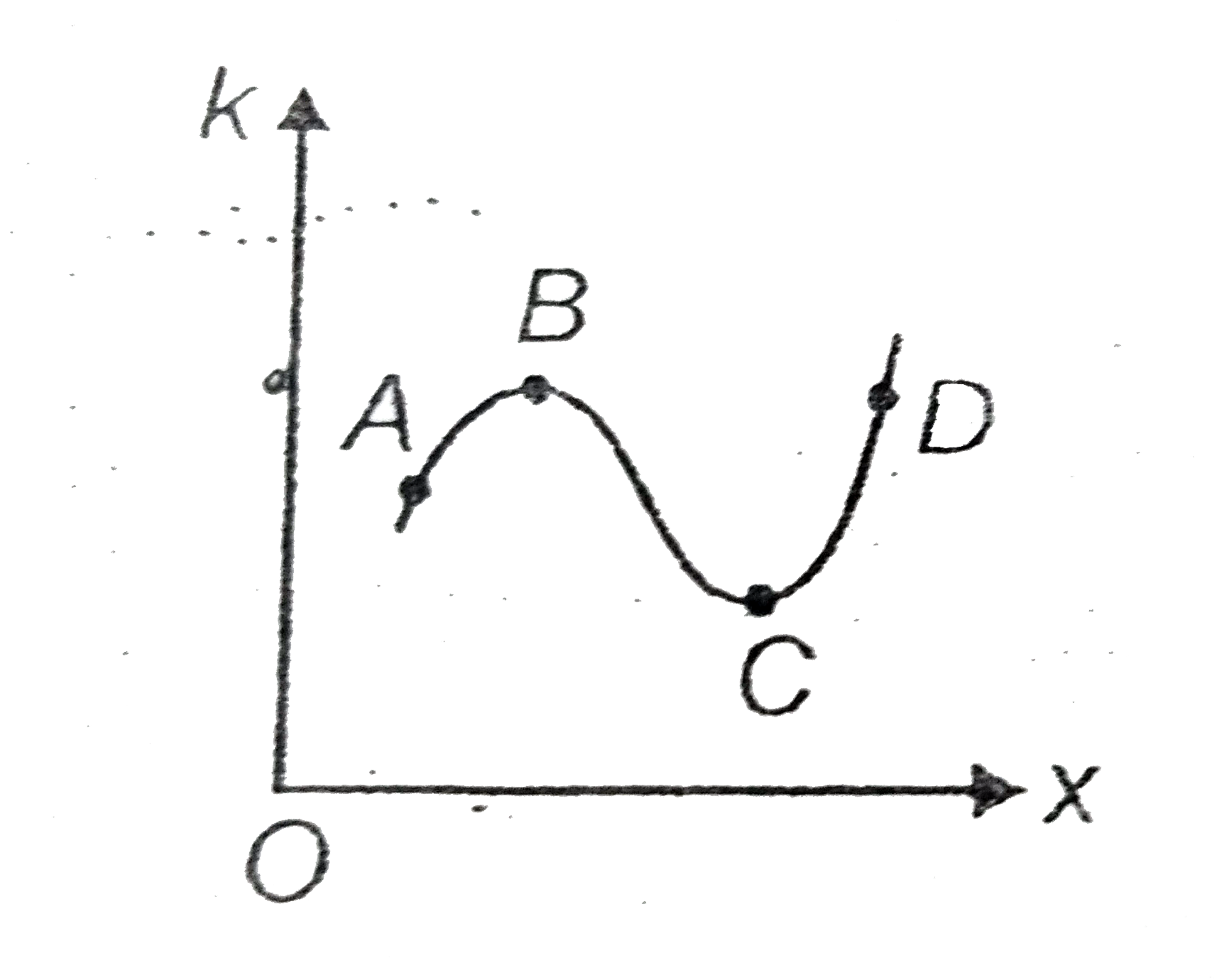
View Solution
Knowledge Check
A particle is moving along x-axis under the action of a force, F which varies with its position (x) as F∝x−1/4. The variation of power due to this force with x is
Ax1/3Bx1/8Cx1/2Dt1/4A particle starts moving from rest along y axis and a variable force F acts on it such that F∞y−15 (y>0). The variation of power P of this force with y is given as
AP∞y15BP∞y−15CP∞y25DP=constantA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (1):Ait is moving along negative X-direction with a speed that is increasing with timeBit is moving along positive X-direction with a speed that is decreasing with timeCit is moving along negative X-direction with a speed that is decreasing with timeDit is moving along positive X-direction with a speed that is increasing with time
Force acting on a particle varies with the distance travelled by the particle as F prop(1)/((x)^(1/3)) then power due to this force varies with as:
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (3) :
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.
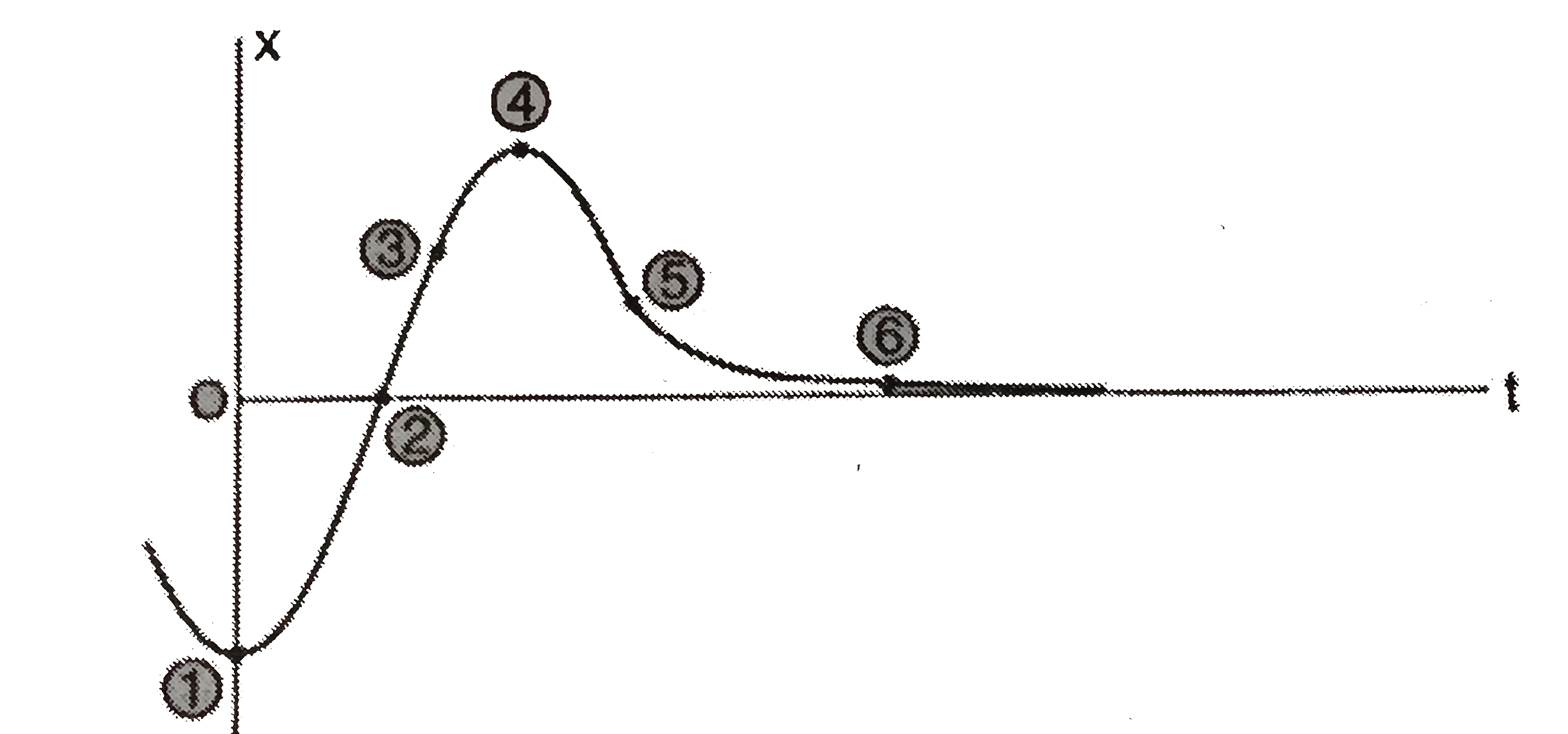
As the particle passes position (6) :
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (2):
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (5) :
View Solution

