A block of mass M is kept on a platform which starts accelerating upwards from rest with a constant acceleration a. During the time interval T, the work done by contact froce on mass M is
(##NARN∃TPHYXIP2C06E09011_Q01##)
12Ma2T2
zero kinetic energy and finite momentum
12M(g+a)2T2
12M(g−a)2T2
The correct Answer is:(3)
To solve the problem of finding the work done by the contact force on a block of mass M kept on a platform that accelerates upwards with a constant acceleration a, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
When the platform accelerates upwards, two forces act on the block:
1. The gravitational force acting downwards, which is Fg=mg.
2. The normal force N exerted by the platform acting upwards.
Step 2: Determine the Normal Force
Since the platform is accelerating upwards, we need to consider the pseudo force acting on the block due to the upward acceleration. The effective force balance can be written as:
N−mg=ma
Rearranging this gives us:
N=mg+ma=m(g+a)
Step 3: Calculate the Displacement of the Block
The displacement s of the block during the time interval T can be calculated using the equation of motion:
s=ut+12at2
Since the initial velocity u=0 (the platform starts from rest), the equation simplifies to:
s=12aT2
Step 4: Calculate the Work Done by the Contact Force
The work done W by the contact force (normal force) on the block can be calculated using the formula:
W=N⋅s
Substituting the values of N and s:
W=(m(g+a))⋅(12aT2)
Thus, the expression for the work done becomes:
W=12m(g+a)aT2
Final Answer
The work done by the contact force on mass M during the time interval T is:
W=12m(g+a)aT2
When the platform accelerates upwards, two forces act on the block:
1. The gravitational force acting downwards, which is Fg=mg.
2. The normal force N exerted by the platform acting upwards.
Since the platform is accelerating upwards, we need to consider the pseudo force acting on the block due to the upward acceleration. The effective force balance can be written as:
N−mg=ma
Rearranging this gives us:
N=mg+ma=m(g+a)
The displacement s of the block during the time interval T can be calculated using the equation of motion:
s=ut+12at2
Since the initial velocity u=0 (the platform starts from rest), the equation simplifies to:
s=12aT2
The work done W by the contact force (normal force) on the block can be calculated using the formula:
W=N⋅s
Substituting the values of N and s:
W=(m(g+a))⋅(12aT2)
Thus, the expression for the work done becomes:
W=12m(g+a)aT2
The work done by the contact force on mass M during the time interval T is:
W=12m(g+a)aT2
Topper's Solved these Questions
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -II (H.W)
Explore 75 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -III
Explore 54 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -1 (H.W)
Explore 60 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-IV
Explore 56 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
Similar Questions
A block of mass M is kept on a platform which is accelerated upward with a constant acceleration 'a' during the time interval T. The work done by normal reaction between the block and platform is

View SolutionA block of mass m is kept on a platform which starts from rest with constant acceleration g/4 upward, as shown in the figure. Work done by normal reaction on block in time t is:
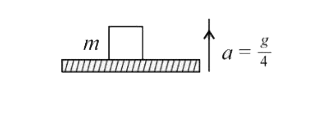
View Solution
Knowledge Check
A block of mass m is kept on a platform Platform starts moving upwards with an acceleration of g2 . Find the work done by the normal force on the block in the first one second.
A3mg22BzeroC3mg28D3mg24A block of mass m is suspended by a light thread from an elevator. The elevator is accelerating upward with uniform acceleration a. The work done by tension on the block during t seconds is (u = 0)
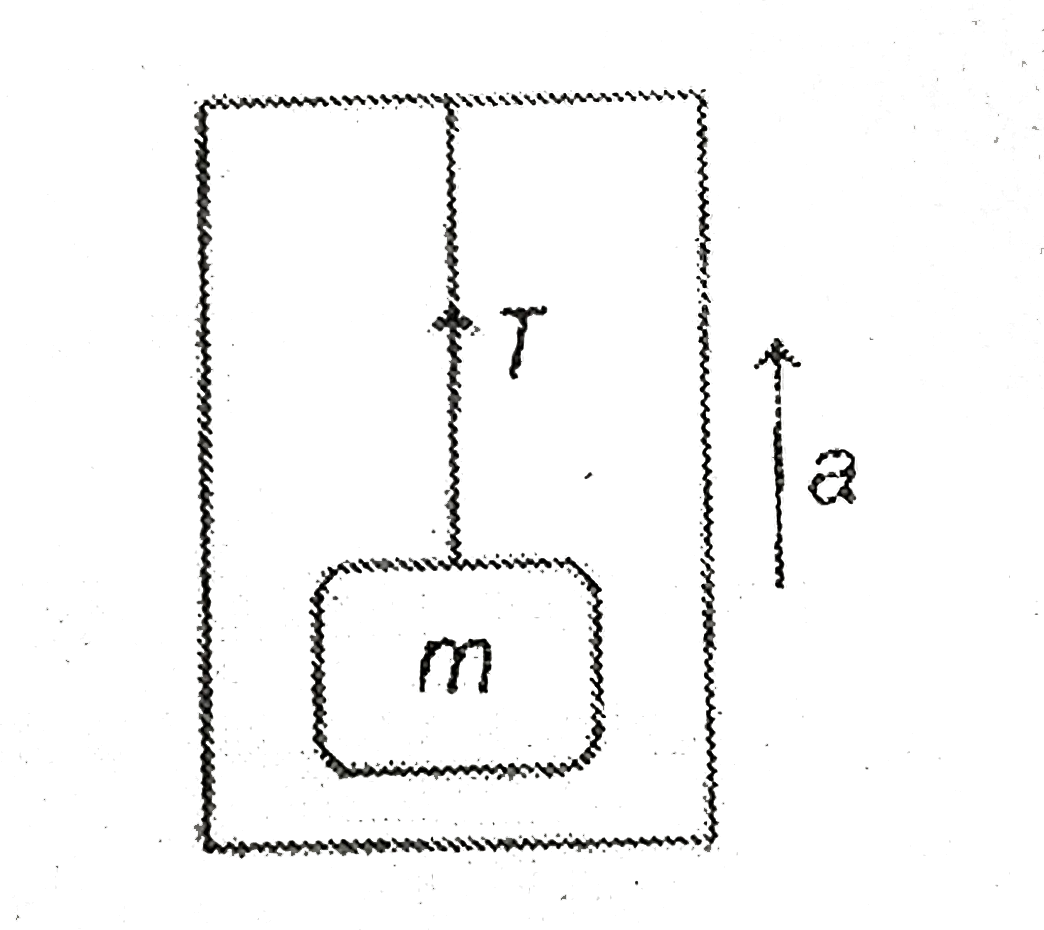 Am2(g+a)at2Bm2(g−a)at2Cm2gat2D0
Am2(g+a)at2Bm2(g−a)at2Cm2gat2D0A block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
Amgd3B−mgd3C23mgdD−23mgd
A block of mass m is kept on a platform which starts from rest with constant acceleration g/2 upward, as shown in fig. Work done by normal reaction on block in time t is :

View SolutionA block of mass m is kept on a platform which starts from rest with constant acceleration g/2 upward, as shown in fig. Work done by normal reaction on block in time t is :

View SolutionA block of mass 2kg is kept inside a lift. Lift starts moving downward with an acceleration of a=12m/s2 .Height of the lift is 4m .Time after which block will strike roof of the lift is?
View SolutionA mass M is lowered with the help of a string by a distance h at a distance acceleration g/2. The work done by the string will be
View SolutionA particle of mass 2kg start motion form rest on a circular path of radius r=4m with constant tangential acceleration 4ms−2. Find the net work done on the particle in initial 1 second.
View Solution

