A vertical spring has a time period of oscillations of T1 with a load m1 at its end. Its time period is T2 when the load is replaced by another of mass m2. The force constant of the spring is
4π2(m1−m2T21−T22)
4π2(m1+m2T21+T22)
2π2(m1+m2T21+T22)
4π2(m1−m2T21+T22)
The correct Answer is:A
To find the force constant k of the spring, we can use the relationship between the time period of oscillation and the mass attached to the spring. The time period T for a mass m attached to a spring with spring constant k is given by the formula:
T=2π√mk
Step 1: Write the equations for the two time periods
For the first mass m1 with time period T1:
T1=2π√m1k
For the second mass m2 with time period T2:
T2=2π√m2k
Step 2: Square both equations
Squaring both equations gives:
T21=4π2m1k(1)
T22=4π2m2k(2)
Step 3: Rearrange both equations to solve for k
From equation (1):
k=4π2m1T21
From equation (2):
k=4π2m2T22
Step 4: Set the two expressions for k equal to each other
Since both expressions represent the same spring constant k:
4π2m1T21=4π2m2T22
Step 5: Cross-multiply to eliminate k
Cross-multiplying gives:
m1T22=m2T21
Step 6: Solve for k in terms of m1,m2,T1, and T2
Now, we can express k in terms of T1 and T2:
k=4π2(m1+m2)T21+T22
Final Result
Thus, the force constant k of the spring is given by:
k=4π2(m1+m2)T21+T22
For the first mass m1 with time period T1:
T1=2π√m1k
T2=2π√m2k
Squaring both equations gives:
T21=4π2m1k(1)
T22=4π2m2k(2)
From equation (1):
k=4π2m1T21
k=4π2m2T22
Since both expressions represent the same spring constant k:
4π2m1T21=4π2m2T22
Cross-multiplying gives:
m1T22=m2T21
Now, we can express k in terms of T1 and T2:
k=4π2(m1+m2)T21+T22
Thus, the force constant k of the spring is given by:
k=4π2(m1+m2)T21+T22
Topper's Solved these Questions
Similar Questions
Derive an expression for the time -period of the horizontal oscillation of a massless loaded spring.
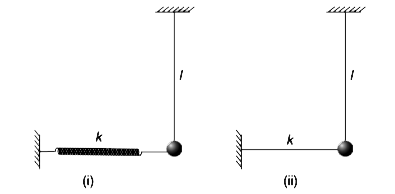
View SolutionA simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
View Solution
Knowledge Check
The time period of oscillations of a block attached to a spring is t1. When the spring is replaced by another spring, the time period of the block is t2. If both the springs are connected in series and the block is made to oscillate using the combination, then the time period of the block is
AT=t1+t2BT2=t21+t22CT−1=t−11+t−12DT−2=t−21+t−22A mass of 1 kg is suspended from a spring. Its time period of oscillation on the earth is T. What will be its time periods at the centre of the earth?
AZeroBTC2TDInfiniteThe graph between period of oscillation (T) and mass attached (m) to a spring will be
A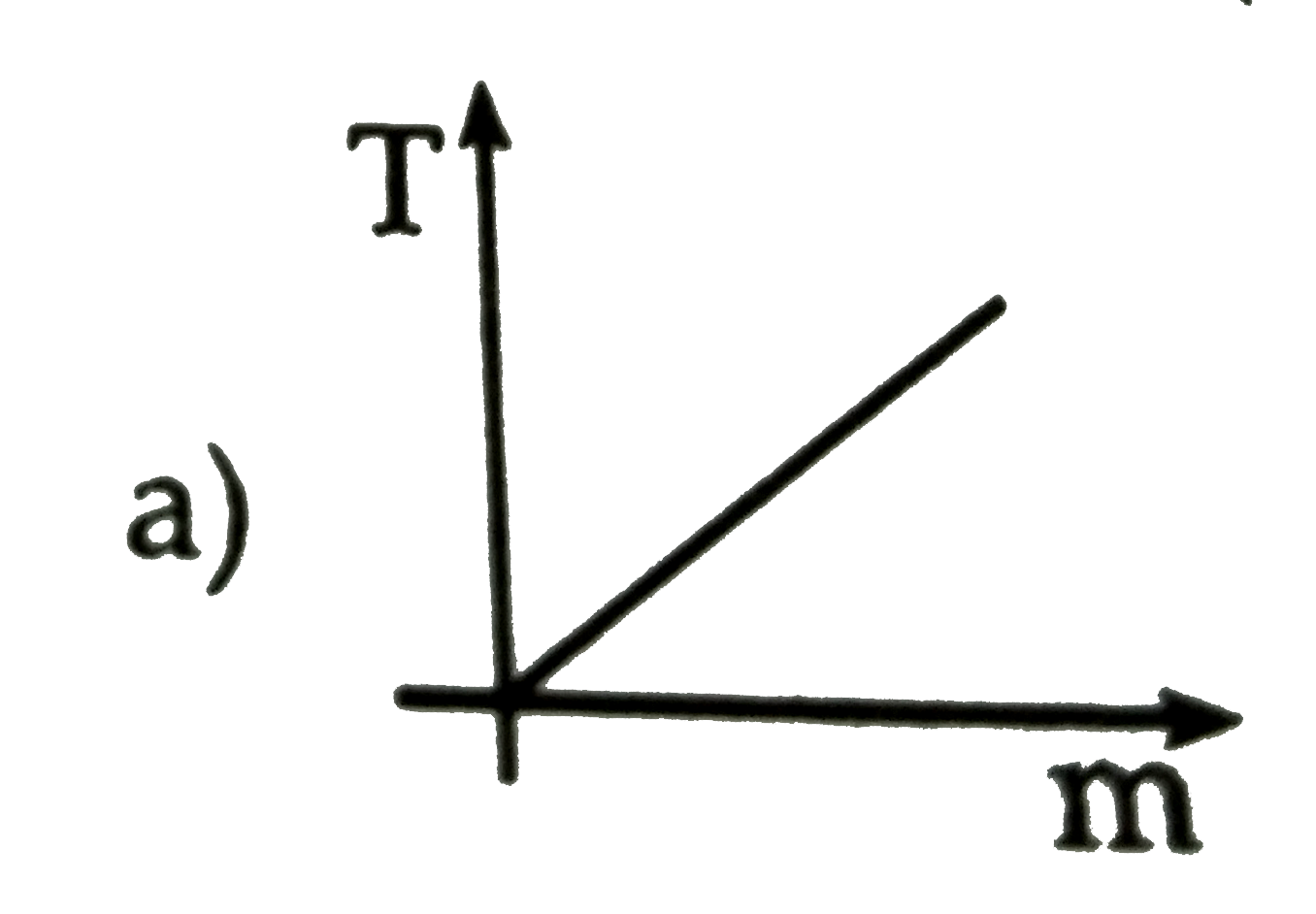 B
B C
C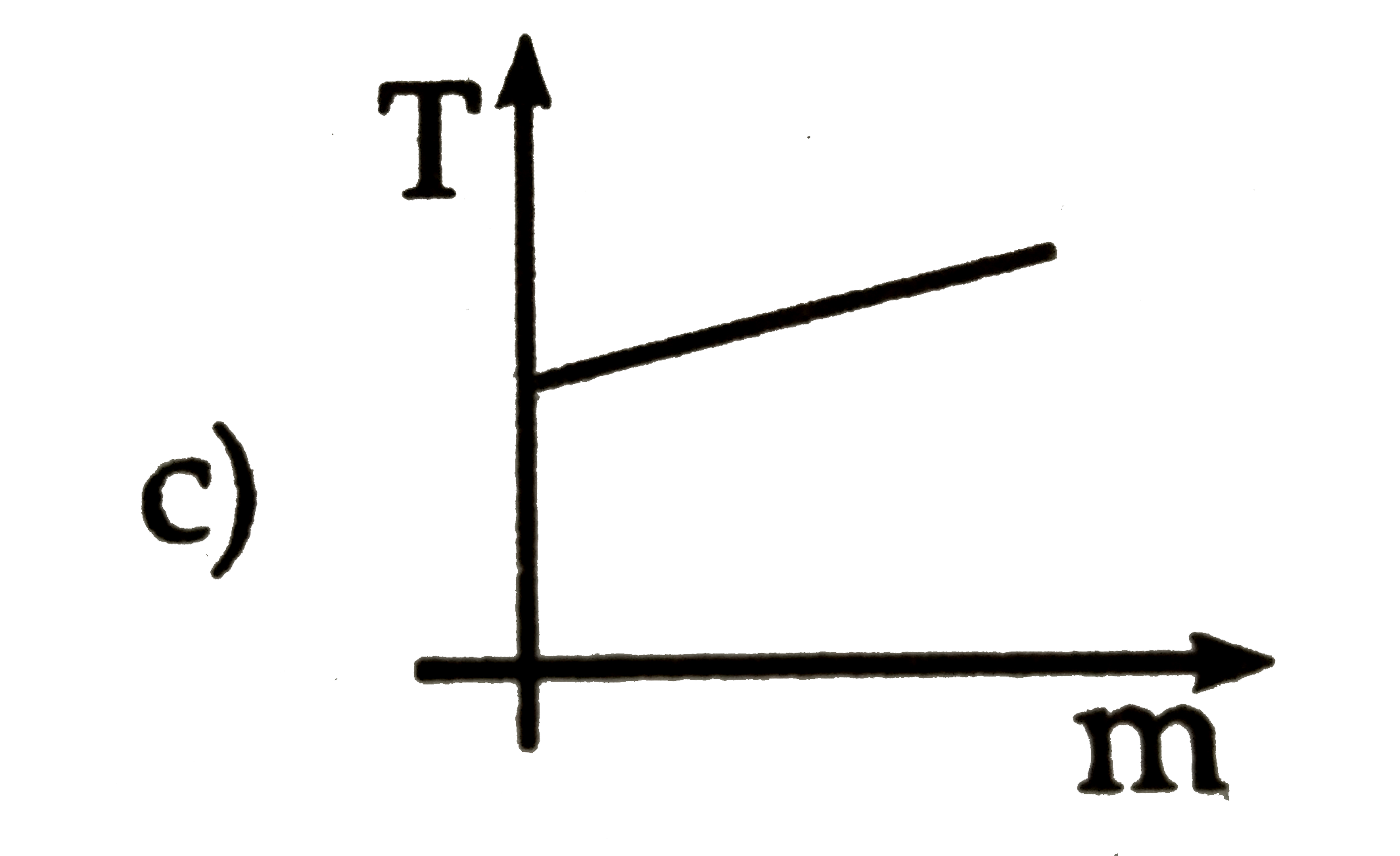 D
D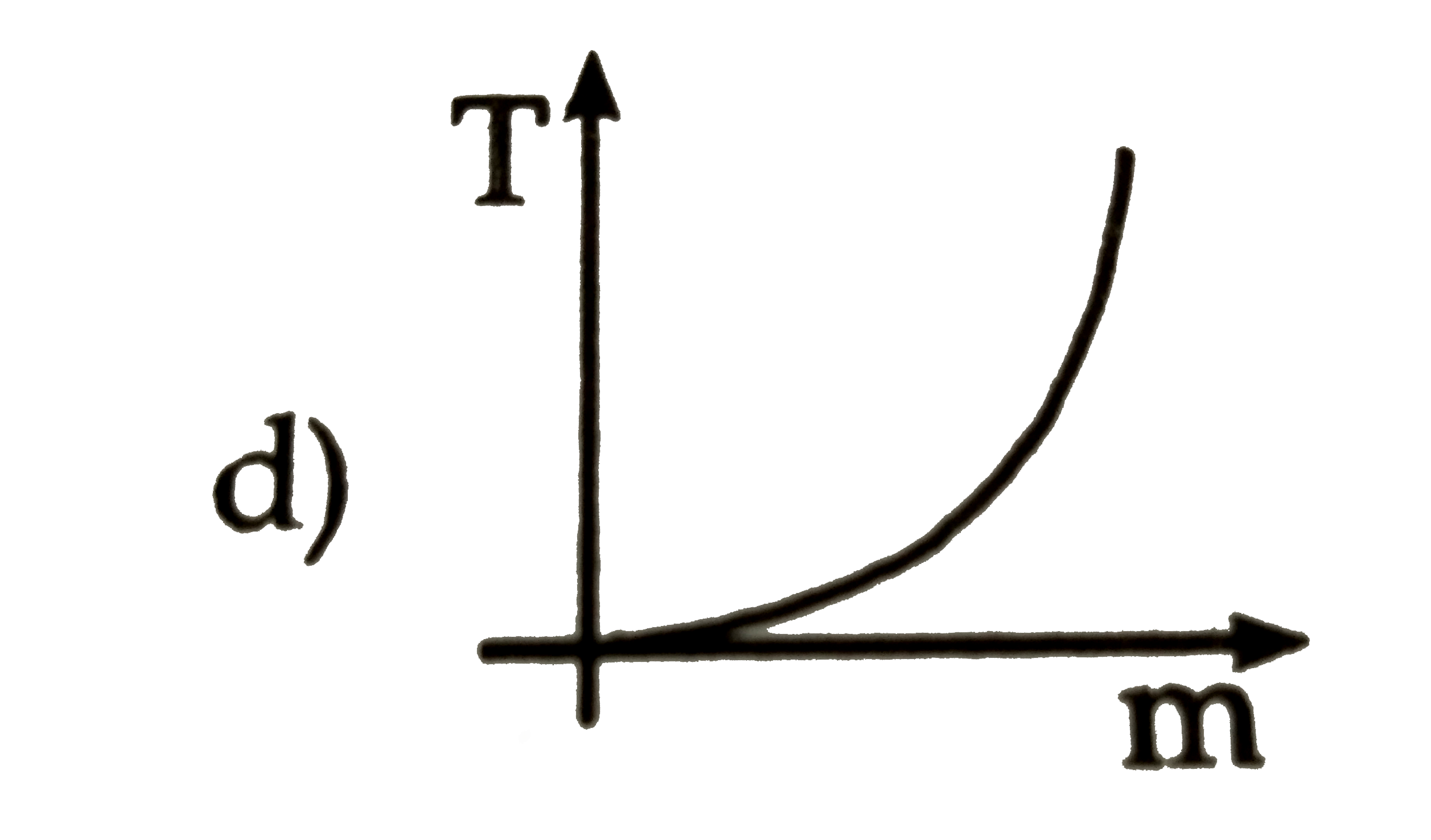
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

View SolutionThe time period of a loaded spring on earth is 6s. On the surface of moon, the time period of the same loaded spring will be
View SolutionA flat spiral spring of force constant k is loaded with mass M and oscillate about vertical with a time period T. Then the mass suspended to the free end is
View SolutionA flat spiral spring of force constant K is loaded with mass M and oscillates vertically with a time period T. Then the mass suspended to the free end is
View SolutionThe time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
View Solution
