Two satellite are revolving around the earth with velocities v1 and v2 and in radii r1 and r2(r1>r2) respectively. Then
v1=v2
v1>v2
v1<v2
V1r1=V2r2
The correct Answer is:C
v=√gr⇒v∝√r
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV40videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -II (H.W.)34videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
Assertion : Two satellites of mass m1&m2(m1>m2) are going around the earth in orbit of raddi s r1andr2(r1>r2) .
Reason : They will have same velocity .View SolutionTwo satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.

For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
If the two have same massView Solution
Knowledge Check
- Question 1 - Select One
Two satellites of masses m1 and m2(m1>m2) are revolving around earth in circular orbits of radii r1 and r2(r1>r2) respectively. Which of the following statements is true regarding their velocities V1 and V2
AV1=V2BV1<V2CV1>V2DV1r1=V2r2 - Question 2 - Select One
A and B are two satellite revolving around the earth in circular orbits with radii RAandRB. Their periods TAandTB are 8 h and 1 h respectively. Then the ratio of (RA/RB) is equal to
A4B8C(8)1/3D√8 - Question 3 - Select One
Two satellites of masses of m1 and m2(m1>m2) are revolving round the earth in circular orbits of radius r1 and r2(r1>r2) respectively. Which of the following statements is true regarding their speeds v1 and v2?
Av1=v2Bv1<v2Cv1>v2Dv1r1=v2r2
Two planets move around the sun. The periodic times and the mean radii of the orbits are T1,T2 and r1r2 respectively. The ratio T1/T2 is equal to
View Solution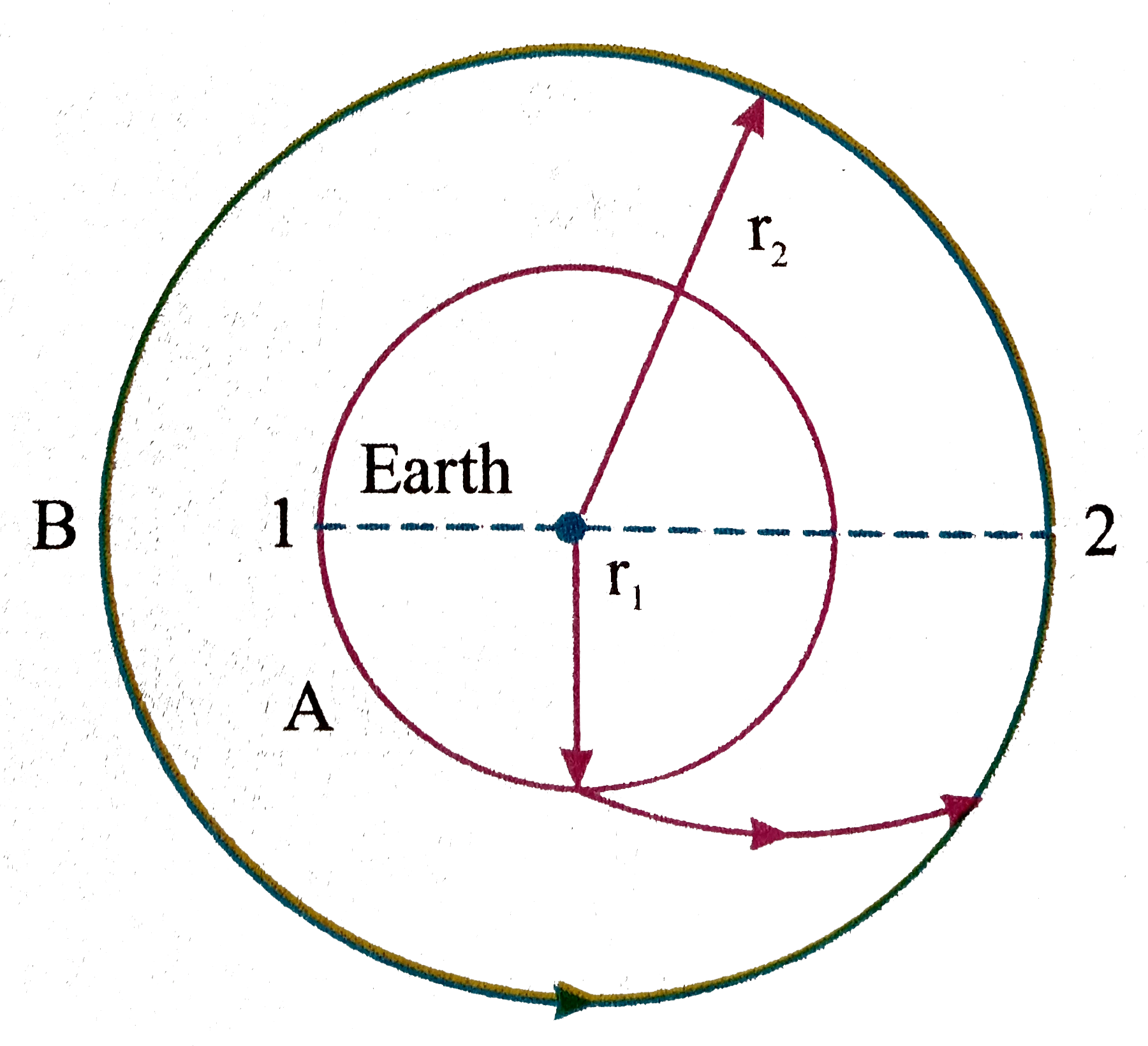
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If r2=3r1 and time period of revolution for B be T then time taken by A in moving from position 1 to position 2 isView SolutionTwo satellites A and B of masses m1 and m2(m1=2m2) are moving in circular orbits of radii r1 and r2(r1=4r2), respectively, around the earth. If their periods are TA and TB, then the ratio TA/TB is
View SolutionTwo planets revolve round the sun with frequencies N1 and N2 revolutions per year. If their average orbital radii be R1 and R2 respectively, then R1/R2 is equal to
View SolutionTwo satellite revolve around the earth in circular orbits at heights h1andh2 above the surface of the earth respectively. If R is radius of the earth, then the ratio of their orbital linear velocities is
View Solution

