Particles of masses and are at a fixed distance apart. If the gravitational field strength at and are and respectively. Then
The correct Answer is:A
To solve the problem, we need to analyze the gravitational field strengths at the positions of two masses, m1 and m2, which are at a fixed distance apart. The gravitational field strength at m1 is denoted as →I1 and at m2 as →I2.
1. Understanding Gravitational Field Strength:
The gravitational field strength →I at a mass due to another mass is given by the formula:
→I=G⋅md2
where G is the gravitational constant, m is the mass creating the field, and d is the distance from the mass to the point where the field is being measured.
2. Gravitational Field Strength at m1:
The gravitational field strength at mass m1 due to mass m2 is:
→I1=G⋅m2d2
This field strength acts towards m2.
3. Gravitational Field Strength at m2:
Similarly, the gravitational field strength at mass m2 due to mass m1 is:
→I2=G⋅m1d2
This field strength acts towards m1.
4. Direction of Gravitational Forces:
The gravitational field strength →I1 at m1 acts towards m2, and →I2 at m2 acts towards m1. Therefore, if we consider the direction of →I1 as positive, then →I2 will be negative when considering the force balance.
5. Applying Newton's Third Law:
According to Newton's third law, the forces exerted by the masses on each other are equal in magnitude and opposite in direction. Thus, we can express the gravitational forces as:
F1=m1⋅→I1andF2=m2⋅(−→I2)
6. Setting Up the Equation:
Since the forces are equal and opposite, we can write:
m1⋅→I1+m2⋅(−→I2)=0
Rearranging gives:
m1⋅→I1−m2⋅→I2=0
7. Conclusion:
Thus, we have derived the relationship:
m1⋅→I1=m2⋅→I2
This corresponds to the option:
m1⋅→I1−m2⋅→I2=0
Final Answer:
The correct answer is:
m1⋅→I1−m2⋅→I2=0
The gravitational field strength →I at a mass due to another mass is given by the formula:
→I=G⋅md2
where G is the gravitational constant, m is the mass creating the field, and d is the distance from the mass to the point where the field is being measured.
The gravitational field strength at mass m1 due to mass m2 is:
→I1=G⋅m2d2
This field strength acts towards m2.
Similarly, the gravitational field strength at mass m2 due to mass m1 is:
→I2=G⋅m1d2
This field strength acts towards m1.
The gravitational field strength →I1 at m1 acts towards m2, and →I2 at m2 acts towards m1. Therefore, if we consider the direction of →I1 as positive, then →I2 will be negative when considering the force balance.
According to Newton's third law, the forces exerted by the masses on each other are equal in magnitude and opposite in direction. Thus, we can express the gravitational forces as:
F1=m1⋅→I1andF2=m2⋅(−→I2)
Since the forces are equal and opposite, we can write:
m1⋅→I1+m2⋅(−→I2)=0
Rearranging gives:
m1⋅→I1−m2⋅→I2=0
Thus, we have derived the relationship:
m1⋅→I1=m2⋅→I2
This corresponds to the option:
m1⋅→I1−m2⋅→I2=0
The correct answer is:
m1⋅→I1−m2⋅→I2=0
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EXERCISE -I (H.W.)
Explore 56 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EXERCISE -II (C.W.)
Explore 38 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EVALUATE YOURSELF-5
Explore 10 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
Two bodies of masses m1 and m2 are placed at a distance r apart. Show that the position where the gravitational field due to them is zero, the potential is given by
−G(m1+m2+2√m1+m2)/r
View SolutionTwo bodies of masses m1andm2 ar placed at a distance r apart. Shows that the position where the gravitational field due to them is zer, the potential is given by
V=−Gr[m1+m2+2√m1m2]
View Solution
Knowledge Check
Particles of masses m1 and m2 are at a fixed distance apart. If the gravitational field strength at m1 and m2 are →I1 and →I2 respectively. Then,
Am1→I1+m2→I2=0Bm1→I2+m2→I1=0Cm1→I1−m2→I2=0Dm1→I2−m2→I1=0Two like poles of strengths m1 and m2 are at far distance apart. The energy repuired to bring them r0 distance apart is
A(μ04πm1m2r0)B(μ08πm1m2r0)C(μ016πm1m2r0)D(μ02πm1m2r0)Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
Aacceleration of both the particles are equal.Bacceleration of the particle of mass m1 is proportional to m1Cacceleration the particle of mass m1 is proportional to m2.Daccelaration of the particle of mass m1 is inversely proportional to m1.
Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.
View SolutionTwo bodies of masses m1andm2 are separated by certain distance. If →F12 is the force on m1 due to m2 and →F21 is the force on m2 due to m1, then
View SolutionTwo bodies of masses M1 and M2, are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
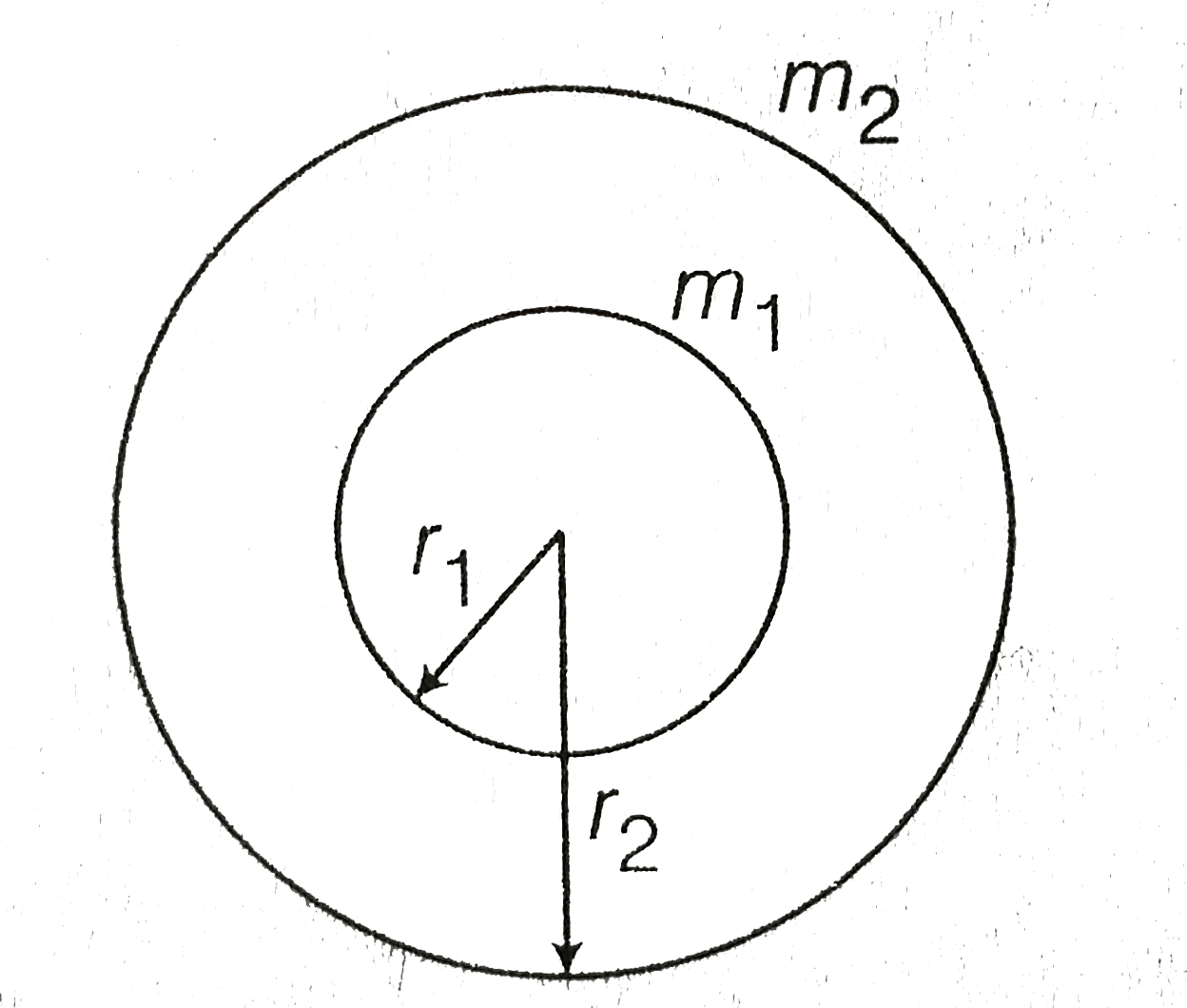
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View Solution
