Four particles A,B,CandD are situated at the cornerst of a square ABCD of side aatt−0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CB~andD along DA. At what time will these particles meet each other ?
dv
√2dv
d2v
d√2v
The correct Answer is:A
T=a2vsin2(πn),(n=4)
Similar Questions
Three boys A,B and C are situated at the vertices of an equilateral triangle of side d at t=0. Each of the boys moves with constant speed v. A always moves towards C and C towards A, At what time and where they meet each other?
View SolutionThree particles A,B,andC are situated at the vertices of an equilateral triangle of side r at t=0. The particle A heads towards B, B towards C, C towards A with constant speeds v. Find the time of their meeting.
View Solution
Knowledge Check
Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
At=dvBt=3d2vCt=2d3vDt=0Three particles A,B and C and situated at the vertices of an equilateral triangle ABC of side of length l at time t=0,Each of the particles move with constant speed u. A always has its velocity along AB,B along BC and C along CA.
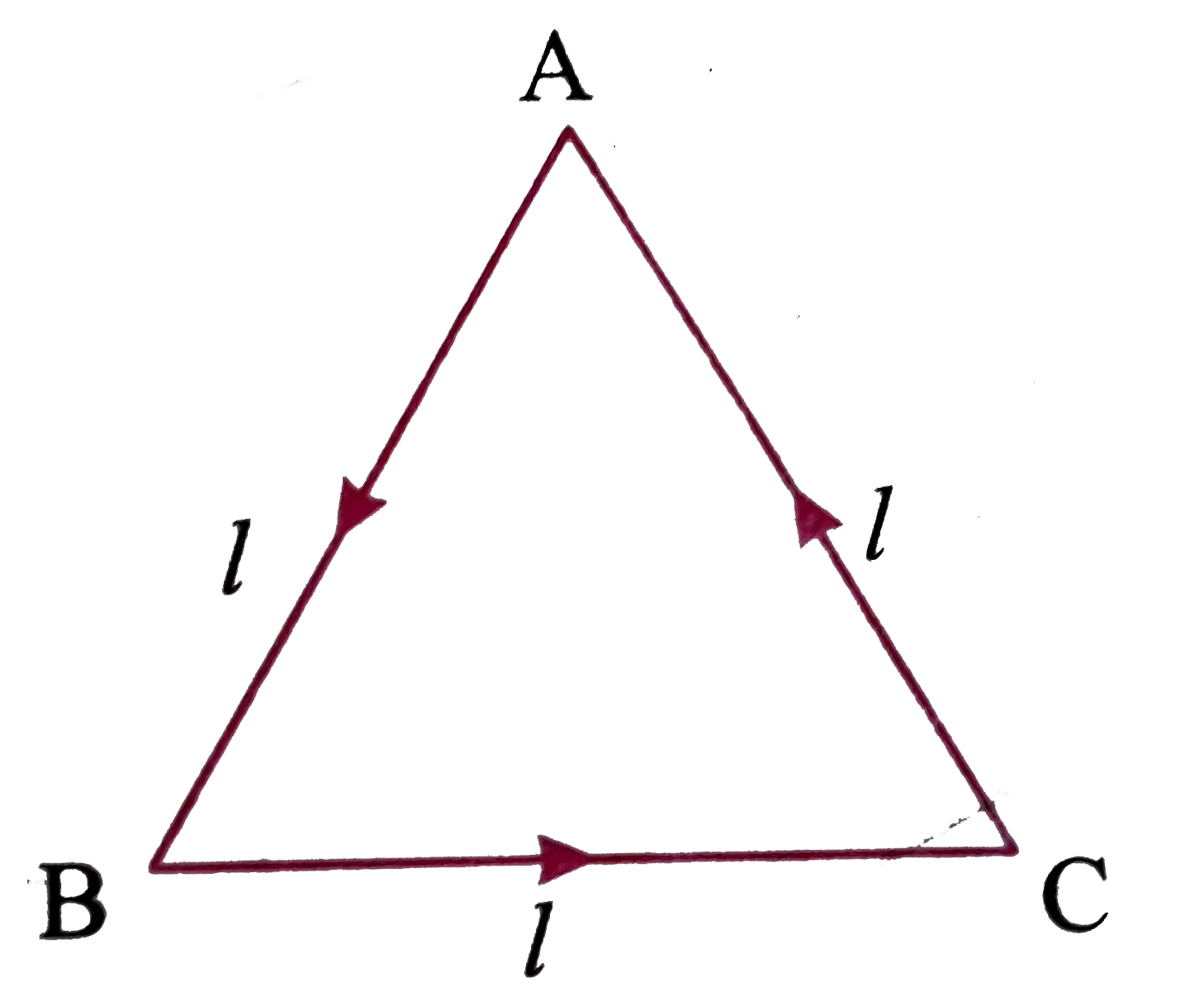 AThe time after which they meet is 2l3uBTotal distance travelled by each particle before they meet is 2l3CAverage velocity during the motion is √3u2DRelative velocity of apporach between any two particles is 3u2
AThe time after which they meet is 2l3uBTotal distance travelled by each particle before they meet is 2l3CAverage velocity during the motion is √3u2DRelative velocity of apporach between any two particles is 3u2If a particle is moving along a circular path with constant speed, then Its motion is
APeriodic and simple harmonicBNon periodicCPeriodic but not simple harmonicDNon periodic but simple harmonic
Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
View SolutionFour particles situated at the corners of a square of side ‘a’ move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.
View SolutionA particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
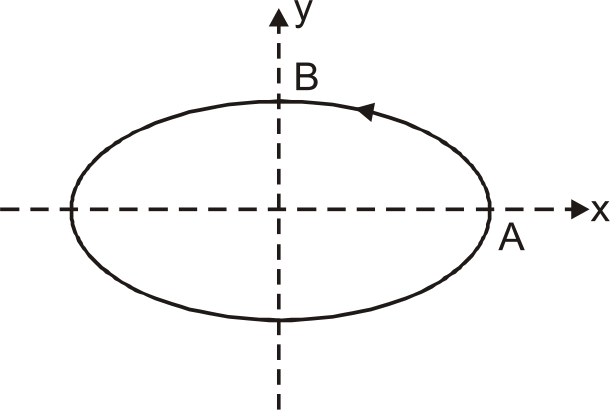
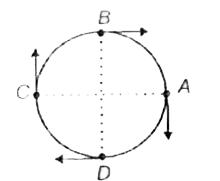
View SolutionFour particles A, B, C and D are moving with constant speed v each at the instant shown relative velocity of A with respect to B, C and D are in directions
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View Solution
