Uranium- 238 decays to thorium-234 with half-life 5×109yr. The resulting nucleus is in the excited state and hence further emits γ-rays to come to the ground state. It emits 20γ-rays per second. The emission rate will drop to 5γ-rays per second in
1.25×109yr
1010yr
10−8yr
1.25×10−9s
The correct Answer is:B
t=2 half lifes,t=nT=2×5××109 years =1010 year
Topper's Solved these Questions
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:EXERCISE-3
Explore 30 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE- 4 One or more than one correct answer type
Explore 13 Videos
Similar Questions
^57Codecays→^57Fe byβ+ -emission.The resulting ^57Feis∈itsexcitedstateandcomes→thegroundstatebyemi∈ggamma−rays.Thehalf−lifeofbeta^+−decayis270daysandtˆofthegamma−emissionis10^(-8)s.Asamp≤of^57Co given 5.0×109gamma rays per second.How much time will elapse before the emission rate of gamma rays drops to 2.5×109 per second ?
View Solution.12N beta decays to an ecited state of .12C, which subsequenctly decays to the ground state with the emission of a 4.43−MeV gamma ray. What is the maxium kinetic energy of the emitted beta particle?
View Solution
Knowledge Check
Assertion: When a nucleus is in an excited state, it can make a transition to a lower energy state by the emission of gamma rays .
Reason: These are energy levels for a nucleus just like there are energy levels in atoms .AIf both assertion and reason are true and reason is the correct explanation of assertion .BIf both assertion and reason are true but reason is not the correct explanation of assertion .CIf assertion is true but reason is false .DIf both assertion and reason are falseGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
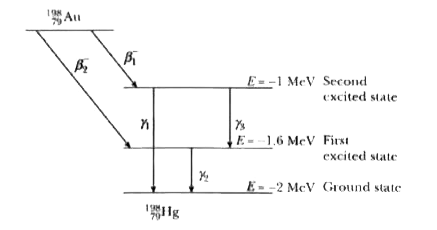
The wavelength of emitted γ - rays is the orderAλ2>λ3>λ1Bλ3>λ2>λ1Cλ1>λ2>λ3Dλ3=λ2=λ1Gold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
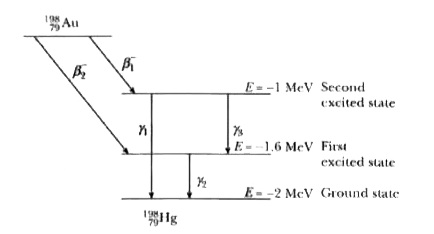
What is the maximum kinetic energy of emitted β1 parricle ?A1.28 MeVB0.77 MeVC1.86 MeVD0.86 MeV
Suppose a .22688Ra nucleus at rest and in ground state undergoes α− decay to a .22286Rn nucleus in its excited state. The kinetic energy of the emitted α particle is found to be 4.44 MeV. .22286Rn nucleus then goes to its ground state by γ-decay. The energy of the emitted γ photon is ___keV.
[Given: atomic mass of .22288Ra=226.005u. atomic mass of 22286Rn=222.000u, atomic mass of α particle =4.000u,1u=931MeV/c2,c is speed of the light].
View SolutionA hydrogen-like gas is kept in a chamber having a slit of width d=0.01mm. The atom of the gas are continuously excited to a certain energy state . The excite electron make transition to lower levels , From the initial excite state to the second excited state and then from the second excited state ground state. In the process of deexcitation, photons are emitted and come out of the container through a slit. The intensity of the photons is observed on a screen placed parallel to the plane of the slit . The ratio of the angular width of the central maximum corresponding to the two transition is 25/2. The angular width of the central maximum due to first transition is 6.4×10−2 radian. Find the atomic number of the gas and the principal quantum number of the inital excited state.
View SolutionThe half life of .23892U is 4.5×109 years. Uranium emits an αparticle to give thorium. Calculate the time required to get the product which contains equal masses of thorium and uranium.
View Solution(a) Find the maximum frequency of the X-rays emitted by an X-ray tube operating at 30kV.
(b) An X-ray tube operates at 20kV. A particular electron loses 5% of its kinetic energy to emit an X-ray photon at the first collision. Find the wavelength corresponding to this photon.
(c ) An X-ray tube is operated at 20kV and the current through the tube is 0.5mA. Find
(i) the number of electrons hitting the target per second,
(ii) the energy falling on the target per second as the kinetic anergy of the electrons and
(iii) the cut-off wavelength of the X-rays emitted.
View SolutionGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
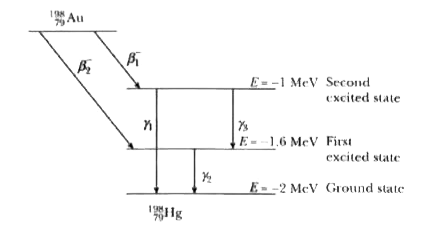
Whatis the maximum kinetic energy of emitted β2 particle?
View Solution