A particle of mass m and positive charge q is released from point A. Its speed is found to be v when it passes through a point B. which of the two points is at higher potential ? What is the potential difference between the points?
To solve the problem, we will use the concepts of electric potential energy and kinetic energy.
1. Understanding the Initial Conditions:
- A particle of mass m and positive charge q is released from point A.
- The initial speed at point A is 0 (since it is released).
- The speed at point B is v.
2. Applying the Conservation of Energy Principle:
- The total mechanical energy of the system remains constant if only conservative forces (like electrostatic forces) are acting on it.
- The initial potential energy at point A will convert into kinetic energy at point B plus the potential energy at point B.
3. Writing the Energy Equation:
- The potential energy at point A can be expressed as UA=qVA (where VA is the electric potential at point A).
- The potential energy at point B can be expressed as UB=qVB (where VB is the electric potential at point B).
- The kinetic energy at point B is given by KB=12mv2.
Therefore, the conservation of energy gives us:
UA=KB+UB
or
qVA=12mv2+qVB
4. Rearranging the Equation:
- Rearranging the equation gives:
qVA−qVB=12mv2
- This can be simplified to:
q(VA−VB)=12mv2
5. Finding the Potential Difference:
- Dividing both sides by q (assuming q≠0):
VA−VB=mv22q
6. Determining Which Point is at Higher Potential:
- Since mv22q is a positive quantity (as m,v,q>0), we conclude that:
VA>VB
- Therefore, point A is at a higher potential than point B.
Final Answer:
- Point A is at a higher potential than point B.
- The potential difference between the points is given by:
VA−VB=mv22q
- A particle of mass m and positive charge q is released from point A.
- The initial speed at point A is 0 (since it is released).
- The speed at point B is v.
- The total mechanical energy of the system remains constant if only conservative forces (like electrostatic forces) are acting on it.
- The initial potential energy at point A will convert into kinetic energy at point B plus the potential energy at point B.
- The potential energy at point A can be expressed as UA=qVA (where VA is the electric potential at point A).
- The potential energy at point B can be expressed as UB=qVB (where VB is the electric potential at point B).
- The kinetic energy at point B is given by KB=12mv2.
UA=KB+UB
or
qVA=12mv2+qVB
- Rearranging the equation gives:
qVA−qVB=12mv2
- This can be simplified to:
q(VA−VB)=12mv2
- Dividing both sides by q (assuming q≠0):
VA−VB=mv22q
- Since mv22q is a positive quantity (as m,v,q>0), we conclude that:
VA>VB
- Therefore, point A is at a higher potential than point B.
- Point A is at a higher potential than point B.
- The potential difference between the points is given by:
VA−VB=mv22q
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-1
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-2
8 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
Similar Questions
Knowledge Check
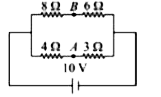
The potential difference between point A & B is
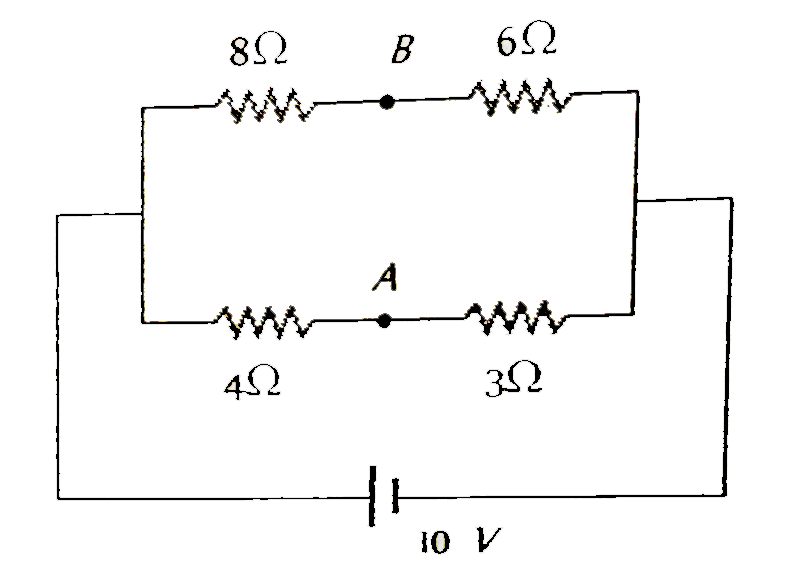 A207VB407VC107VD0
A207VB407VC107VD0The potential difference between point A and B is
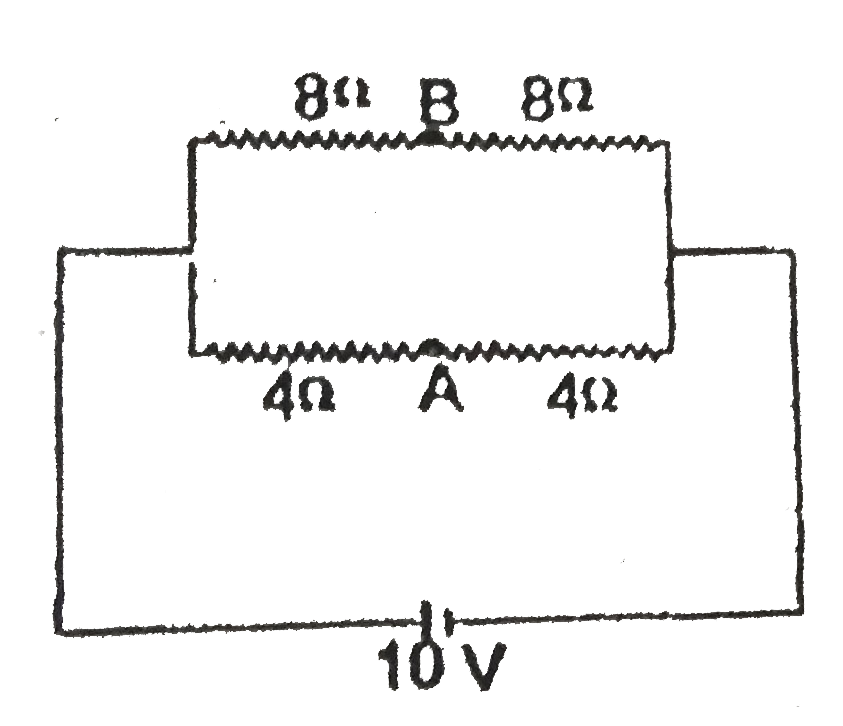 A207VB407VC107VDzero
A207VB407VC107VDzero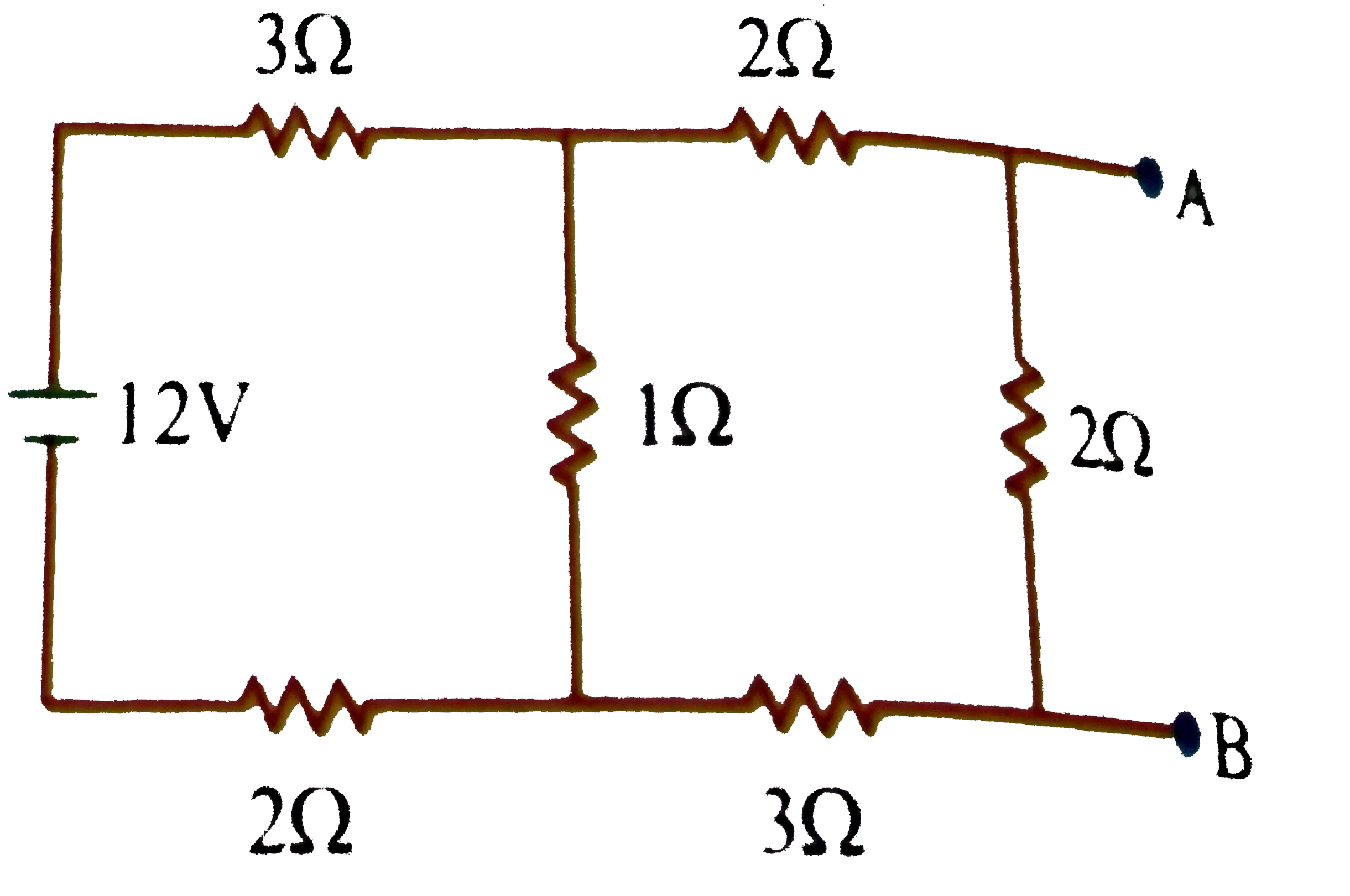
The potential difference between points A and B isA1.50VB2.50VC1.00VD0.50V
What is meant by saying that the potential difference between two points is 1 V?
View SolutionThe potential difference between points A and B is
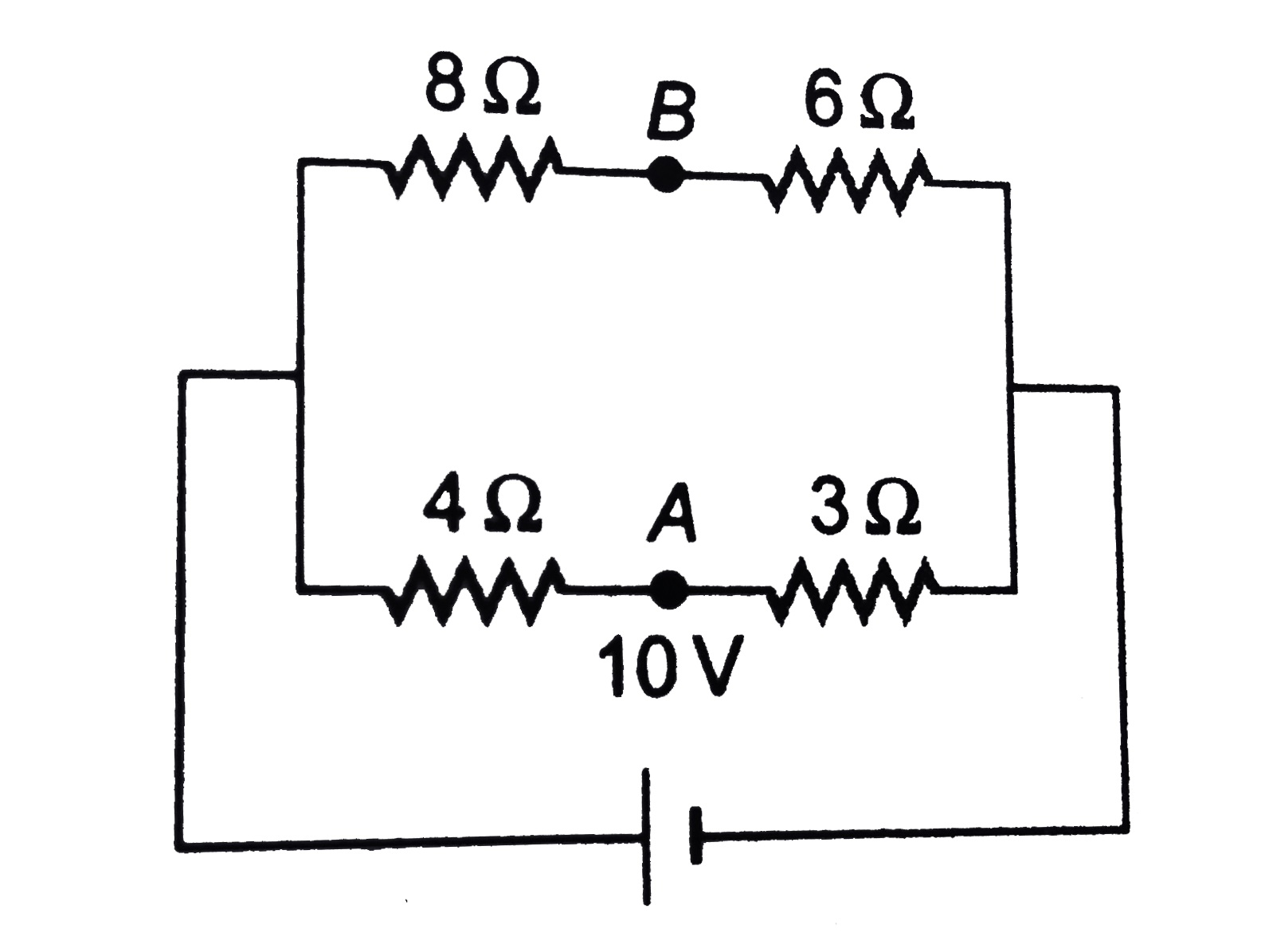
View SolutionThe potential difference between points A and B is:
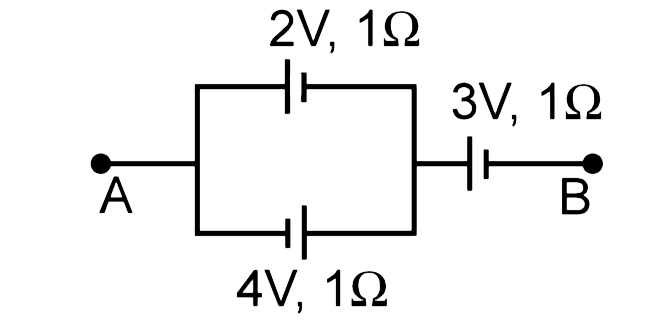
View SolutionThe potential difference between points A and B is -
View SolutionThe potential difference between two points also called
View Solution
