In a region of uniform electric field, as an electron travels from A to B, it slows from
vA=6.1×106m/s to vB=4.5×106m/s. The potential change
ΔV=VB−VA in volts nearly.
18
−18
+48
−48
The correct Answer is:D
To find the potential change ΔV=VB−VA as the electron travels from point A to point B in a uniform electric field, we can use the principle of conservation of energy. The kinetic energy lost by the electron will be equal to the potential energy gained.
1. Identify the given values:
- Initial velocity vA=6.1×106m/s
- Final velocity vB=4.5×106m/s
- Mass of the electron m=9.1×10−31kg
2. Calculate the initial kinetic energy (KE) at point A:
KEA=12mv2A=12(9.1×10−31)(6.1×106)2
3. Calculate the final kinetic energy (KE) at point B:
KEB=12mv2B=12(9.1×10−31)(4.5×106)2
4. Calculate the change in kinetic energy (ΔKE):
ΔKE=KEA−KEB
5. Substituting the values:
KEA=12(9.1×10−31)(6.12×1012)=12(9.1×10−31)(37.21×1012)=1.69×10−18J
KEB=12(9.1×10−31)(4.52×1012)=12(9.1×10−31)(20.25×1012)=9.19×10−19J
ΔKE=1.69×10−18−9.19×10−19=7.71×10−19J
6. Relate the change in kinetic energy to the change in potential energy (ΔU):
ΔU=−ΔKE
7. Calculate the change in potential (ΔV) using the relation ΔU=qΔV:
- The charge of the electron q=−1.6×10−19C
ΔV=ΔUq=−ΔKE−1.6×10−19=7.71×10−191.6×10−19≈48.19V
8. Determine the final result for ΔV:
ΔV=VB−VA≈−48.19V
Final Answer:
The potential change ΔV=VB−VA is approximately −48.19V.
- Initial velocity vA=6.1×106m/s
- Final velocity vB=4.5×106m/s
- Mass of the electron m=9.1×10−31kg
KEA=12mv2A=12(9.1×10−31)(6.1×106)2
KEB=12mv2B=12(9.1×10−31)(4.5×106)2
ΔKE=KEA−KEB
KEA=12(9.1×10−31)(6.12×1012)=12(9.1×10−31)(37.21×1012)=1.69×10−18J
KEB=12(9.1×10−31)(4.52×1012)=12(9.1×10−31)(20.25×1012)=9.19×10−19J
ΔKE=1.69×10−18−9.19×10−19=7.71×10−19J
ΔU=−ΔKE
- The charge of the electron q=−1.6×10−19C
ΔV=ΔUq=−ΔKE−1.6×10−19=7.71×10−191.6×10−19≈48.19V
ΔV=VB−VA≈−48.19V
The potential change ΔV=VB−VA is approximately −48.19V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Evaluate yourself-2
Explore 8 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Evaluate yourself-3
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- ELECTROMAGNETIC WAVES Book:NARAYNAChapter:ELECTROMAGNETIC WAVES Exercise:EXERCISE -4
Explore 15 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
Similar Questions
Knowledge Check
In a region of uniform electric field , as an electron travels from A to B, it slows from uA=6.1×106m/s to uB=4.5×106m/s . What is its potential change ΔV=VB−VA in volts ?
A18B−18C+48D−48In a region of uniform electric field as an electron travels from A to B it slows from UA=6.1×106m/stoUB=4.5×106 m/s . What is its potential change ΔV=VB−VA in volts ?
A18B−18C+48D−48In uniform electric field E=10N/C, find

a. VA−VB , b. VB−VCA−10V and 20VB10V and −10VC30V and 20VD−10V and 40V
A uniform electric field of 100Vm−1 is directed at 30∘ with the positive x - axis as shown in (Fig. 3.153). OA=2m and OB=4m.
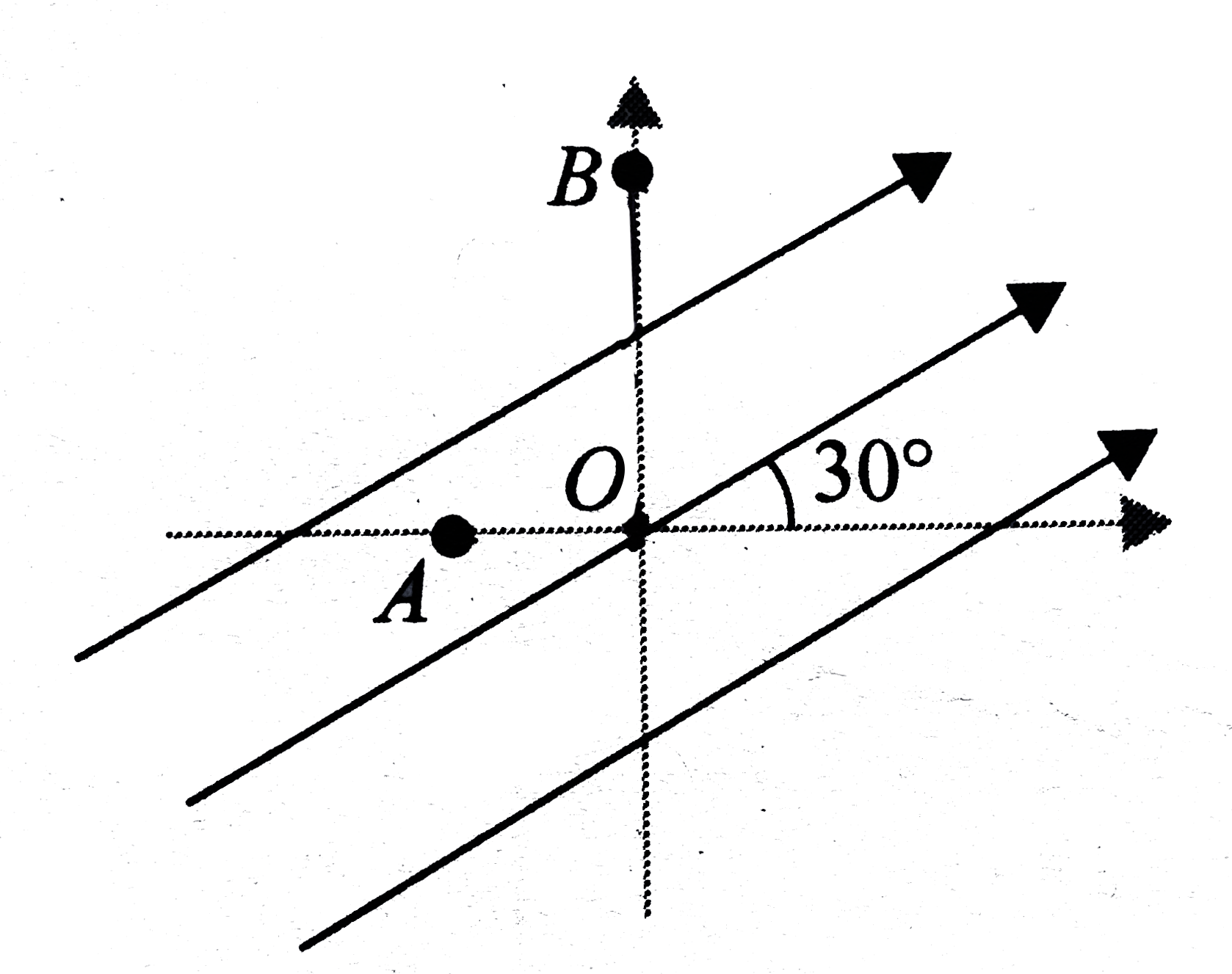 .
.
The potential difference VB−VA is.
View SolutionThe amplitude of the electric field of a plane electromagnetic wave in air is 6.0×10−4Vm−1. The amplitude of the magnetic field will be
View SolutionIn a certain region of space a uniform and constant electric field and a magnetic field parallel to each other are present. A proton is fired from a point A in the field with speed v=4×104m/s at an angle of α with the field direction. The proton reaches a point B in the field where its velocity makes an angle β with the field direction. If sinαsinβ=√3. Find the electric potential difference between the points A and B. Take mp(mass of proton) =1.6×10−27kg and c(magnitude of electronic charge)=1.6×1019C.
View SolutionAn electron traveling in a uniform electric field passes from a region of potential V1 to a region of higher potential V2. Then

View SolutionThe energy of incident radiation, which emits the electrons with a velocity of 2.5×106 m/s and work function 1.8 e V , is
View Solution