Find the component of →r in the directioln of →a :-
(→r.→a)→aa2
(→r.→a)→aa
(→r.→a)→rr
(→r.→a)→rr2
The correct Answer is:A
Step by step video, text & image solution for Find the component of vecr in the directioln of veca :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-2) Multiple Correct Type Questions.
Explore 7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-2) Comprehension Type Questions.
Explore 9 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-1) Matrix match type Questions.
Explore 4 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:MATHS
Explore 18 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Previous Year Questions)
Explore 7 Videos
Similar Questions
Given →a=ˆi+2ˆj+ˆk,→b=−ˆi+2ˆj+ˆkand→c=3ˆi+ˆj. Find a unity vector in the directionof resultant of these vectors. Also find a vector →r which is normal to both →aand→b. What is the inclination of →rand→c?
View SolutionIf →b is not perpendicular to →c . Then find the vector →r satisfying the equation →r×→b=→a×→band→r.→c=0
View Solution
Knowledge Check
If →a=ˆi−2ˆj+3ˆk and →b=−3ˆi+ˆj−ˆk and →r×→a=→b×→a,→r×→b=→a=→b then a unit vector in the direction of →r is:
A13(−2ˆi+ˆj−ˆk)B13(−2ˆi−ˆj+2ˆk)C13(−2ˆi−ˆj−2ˆk)Dnone of theseThe component of →A along →B is √3 times that of the component of →B along →A. Then A:B is
A1:√3B√3:1C2:√3D√3:2The equation of the plane which contains the origin and the line of intersectio of the plane →r.→a=d1 and →r.→b=d2 is
A→r.(d1→a−d2→b)=0B→r.(d1→a+d2→b)=0C→r.(d2→a+d1→b)=0D→r.(d2→a−d2→b)=0
If →b is not perpendicular to →c . Then find the vector →r satisfying the equation →r×→b=→a×→band→r.→c=0
View SolutionFind the components of a vector →R along two straight lines stiuated at both sides of the vector→R making angles α and β with it.
View SolutionThe two vectors →a and →b have equal magnitudes of 10.0 m and the angles are θ1=30∘andθ2=105∘. Find the (a ) x and (b) y components of their vector sum →r,(c ) the magnitude oof →r makes with the positive direction of the x axis.
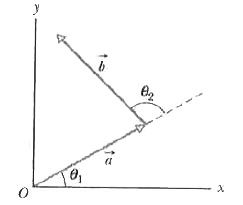
View SolutionShow that the components of →b parallel to →a and perpendicular to it are (→a.→b)→a→a2and((→a×→b)→a))a2 respectively.
View SolutionLet |A|=1,∣∣→b∣∣=4 and →a×→r+→b=→r. If the projection of →r along →a is 2, then the projection of →r along →b is
View Solution