Which of the following graph represents relation between the image position (v) and object position (u) from the concave lens.
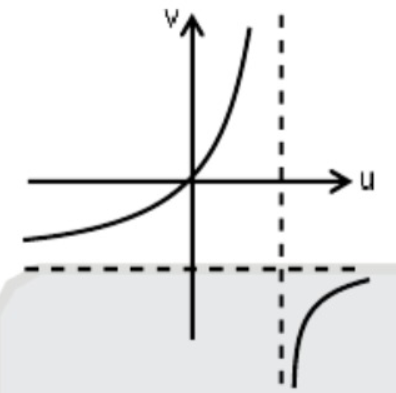
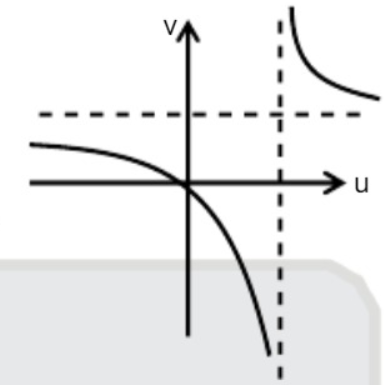
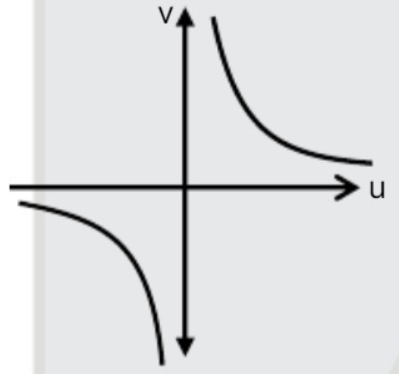
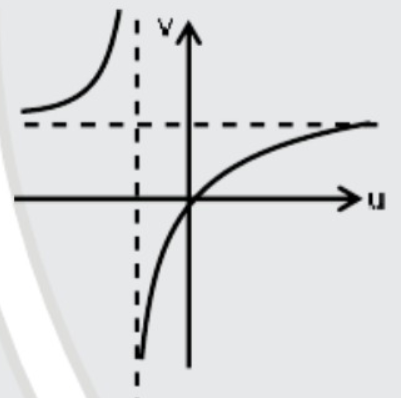
The correct Answer is:A
To determine the relationship between the image position (v) and object position (u) for a concave lens, we can follow these steps:
1. Understand the Lens Formula:
The lens formula is given by:
1v−1u=1f
For a concave lens, the focal length (f) is negative.
2. Identify the Sign Conventions:
- Object distance (u) is negative when the object is on the same side as the incoming light (which is the case for a concave lens).
- Image distance (v) is also negative for virtual images formed by concave lenses.
3. Analyze Different Object Positions:
- When u = -∞: The image forms at v = -f (which is a finite distance on the same side as the object).
- When u = 0: The image also forms at the origin (v = 0).
- When u = -f: The image will be at v = -∞ (the image moves infinitely far away).
- When u = -2f: The image will be at v = -2f (still on the same side as the object but at a finite distance).
4. Plot the Points:
- Plot the points on a graph where:
- For u=−∞, v=−f
- For u=0, v=0
- For u=−f, v=−∞
- For u=−2f, v=−2f
5. Draw the Curve:
- Connect the points smoothly to represent the relationship. The graph will start from (−∞,−f) and curve towards (0,0), then continue to (−2f,−2f) and approach (−∞,−f).
6. Identify the Correct Graph:
- Compare the drawn curve with the provided options to identify which graph accurately represents the relationship between image position (v) and object position (u) for a concave lens.
The lens formula is given by:
1v−1u=1f
For a concave lens, the focal length (f) is negative.
- Object distance (u) is negative when the object is on the same side as the incoming light (which is the case for a concave lens).
- Image distance (v) is also negative for virtual images formed by concave lenses.
- When u = -∞: The image forms at v = -f (which is a finite distance on the same side as the object).
- When u = 0: The image also forms at the origin (v = 0).
- When u = -f: The image will be at v = -∞ (the image moves infinitely far away).
- When u = -2f: The image will be at v = -2f (still on the same side as the object but at a finite distance).
- Plot the points on a graph where:
- For u=−∞, v=−f
- For u=0, v=0
- For u=−f, v=−∞
- For u=−2f, v=−2f
- Connect the points smoothly to represent the relationship. The graph will start from (−∞,−f) and curve towards (0,0), then continue to (−2f,−2f) and approach (−∞,−f).
- Compare the drawn curve with the provided options to identify which graph accurately represents the relationship between image position (v) and object position (u) for a concave lens.
Topper's Solved these Questions
Similar Questions
Which of the following form(s) a virtual and erect image for all positions of the object?
(1) Convex lens
(2) Concave lens
(3) Convex mirror
(4) Concave mirror
View SolutionFor a concave lens of focal length f, the relation between object and image distance u and v, respectively, from its pole can best be represented by (u = v is the reference line) :
View Solution
Knowledge Check
The graph between the image distance (v ) and object distance (u) from the convex lens is
A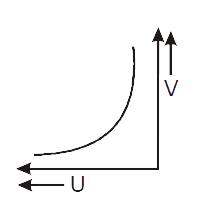 B
B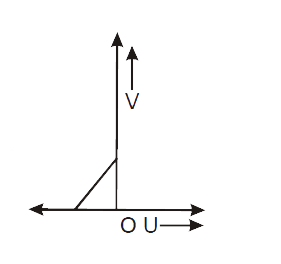 C
C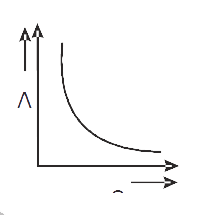 D
D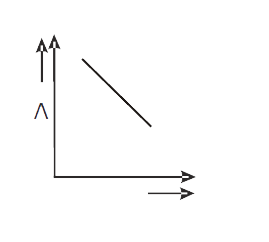
Which of the following graph represents v/f vs u/f graph for a virtual erect image by a diverging lens?
A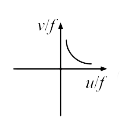 B
B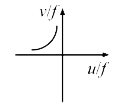 C
C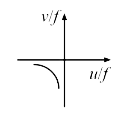 D
D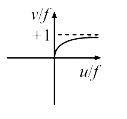
Which of the following can form a virtual image which is always smaller than the object?
AA and BBB and CCA and CDB and D
Giving reasons, the 'signs' (positive or negative) which can be given to the following :
(a) object distance
(b) image distances
( c) image distances
(u) for a concave mirror or convex mirror
(v) for a concave mirror (v) for a convex mirror
View Solution(i) Rohit claims to have obtained an image twice the size of object with a concave lens. Is he correct? Give reason for your answer.
(ii) Where should an object be placed in case of a convex lens to form an image of same size as of the object? Show with the help of ray diagram the position and the nature of the image formed.
(iii) With teh help of ray diagram, illustrate the change in position, nature and size of the image formed if the convex lens in case of (ii) is replaced by concave lens of same focal length.
View SolutionCalculate the position of the image of an object when placed at
(a) focus of a convex lens.
(b) focus of a concave lens.
View SolutionGraph of position of image vs position of point object from a convex lens is shown. Then, focal length of the lens is
_E01_287_Q01.png)
View SolutionThe graph showing correctly the variation of image distance (v) as a function of object distance (u) in case of a concave mirror is
View Solution
