Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of $Δ A B C$ .
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do you observe?
(v) If $A (x_{1}, y_{1}),$ $B (x_{2}, y_{2})$ and $C (x_{3}, y_{3})$ are the vertices of ∆ ABC, find the coordinates of the centroid of the triangle.

Video Solution

Text Solution

Verified by Experts

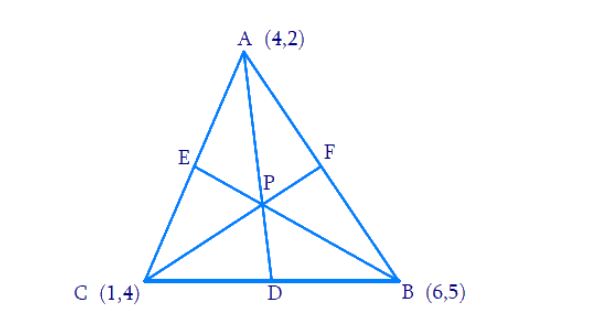
i) Let AD be the median of the triangle ABC
Hence D is the midpoint of BC which can be found using the Mid Point formula.
$M = [\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2}]$
Coordinates of $D = [\frac{6 + 1}{2}, \frac{5 + 4}{2}]$
$= [\frac{7}{2}, \frac{9}{2}]$
ii) $(# # X_{07}_E 04_{07}_s 02 # #)$
Point P divides the side AD in a ratio $m : n = 2 : 1 .$
$(# # X_{07}_E 04_{07}_s 03 # #)$
By Section formula
$P (x, y) = [m x_{2} + n \frac{x_{1}}{m + n}, m y_{2} + n \frac{y_{1}}{m + n}]$
Coordinates of $P = ⎡ ⎣ \frac{2 \times \frac{7}{2} + 1 \times 4}{2 + 1}, \frac{2 \times \frac{9}{2} + 1 \times 2}{2 + 1} ⎤ ⎦$
$= [\frac{11}{3}, \frac{11}{3}]$
(iii) Let's draw the figure,
The Median BE of the triangle will divide the side AC into two equal parts.
Therefore, E is the mid-point of side AC. The co-ordinates of E can be calculated using the Mid-Point Formula.
$M = [\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2}]$
Coordinates of $E = [\frac{4 + 1}{2}, \frac{2 + 4}{2}] = [\frac{5}{2}, 3]$
Point Q divides the side BE in a ratio 2:1.
By Section formula
$P (x, y) = [m x_{2} + n \frac{x_{1}}{m} + n, m y_{2} + n \frac{y_{1}}{m} + n]$ .....Equation(1)
Coordinates of $Q = ⎡ ⎣ \frac{2 \times \frac{5}{2} + 1 \times 6}{2 + 1}, \frac{2 \times 3 + 1 \times 5}{2 + 1} ⎤ ⎦$
$= [\frac{11}{3}, \frac{11}{3}]$
The Median CF of the triangle will divide the side AB into two equal parts.
Therefore, F is the mid-point of side AB. The co-ordinates of F can be calculated using the Mid-Point Formula.
Coordinates of $F = [\frac{4 + 6}{2}, \frac{2 + 5}{2}]$
$= [5, \frac{7}{2}]$
$(# # X_{07}_E 04_{07}_s 04 # #)$
Point R divides the side CF in a ratio 2:1
By Section formula
$P (x, y) = [m x_{2} + n \frac{x_{1}}{m} + n, m y_{2} + n \frac{y_{1}}{m} + n]$ .....Equation(1) Coordinates of $R = ⎡ ⎣ \frac{2 \times 5 + 1 \times 1}{2 + 1}, \frac{2 \times \frac{7}{2} + 1 \times 4}{2 + 1} ⎤ ⎦$
$= [\frac{11}{3}, \frac{11}{3}]$
(iv) It can be observed that the coordinates of points P, Q, R are the same.
Therefore, all these are representing the same point on the plane that is, the centroid of the triangle.
(v) Consider a triangle, $Δ A B C$ , having its vertices as $A (x_{1}, y_{1}), B (x_{2}, y_{2})$ , and $C (x_{3}, y_{3})$
The median AD of the triangle will divide the side BC into two equal parts.
Therefore, D is the mid-point of side BC.
The coordinates of D can be calculated using the Mid-Point Formula.
$D = [\frac{x_{2} + x_{3}}{2}, \frac{y_{2} + y_{3}}{2}]$
Let the centroid of this triangle be O.
Point O divides the side AD in a ratio of 2:1.
Coordinates of $O = ⎡ ⎢ ⎣ \frac{2 \times \frac{x_{2} + x_{3}}{2} + 1 \times x_{1}}{2 + 1}, \frac{2 \times \frac{y_{2} + y_{3}}{2} + 1 \times y_{1}}{2 + 1} ⎤ ⎥ ⎦$
$= [\frac{x_{1} + x_{2} + x_{3}}{3}, \frac{y_{1} + y_{2} + y_{3}}{3}]$

Updated on:21/07/2023

$A (4, 2), B (6, 5)$ and $C (1, 4)$ are the vertices of $A B C$ . Find the coordinates of the points $Q$ on median $B E$ such that $B Q : Q E = 2 : 1$
AQ= $(\frac{11}{3}, \frac{11}{3})$
BQ= $(\frac{10}{3}, \frac{11}{3})$
CQ= $(\frac{11}{3}, \frac{10}{3})$
DQ= $(\frac{10}{3}, \frac{10}{3})$
If A(4, 2), B(6, 5) and C(1, 4) be the vertices of $Δ A B C$ and AD is a median, then the coordinates of D are
A $(\frac{5}{2}, 3)$
B $(5, \frac{7}{2})$
C $(\frac{7}{2}, \frac{9}{2})$
Dnone of these