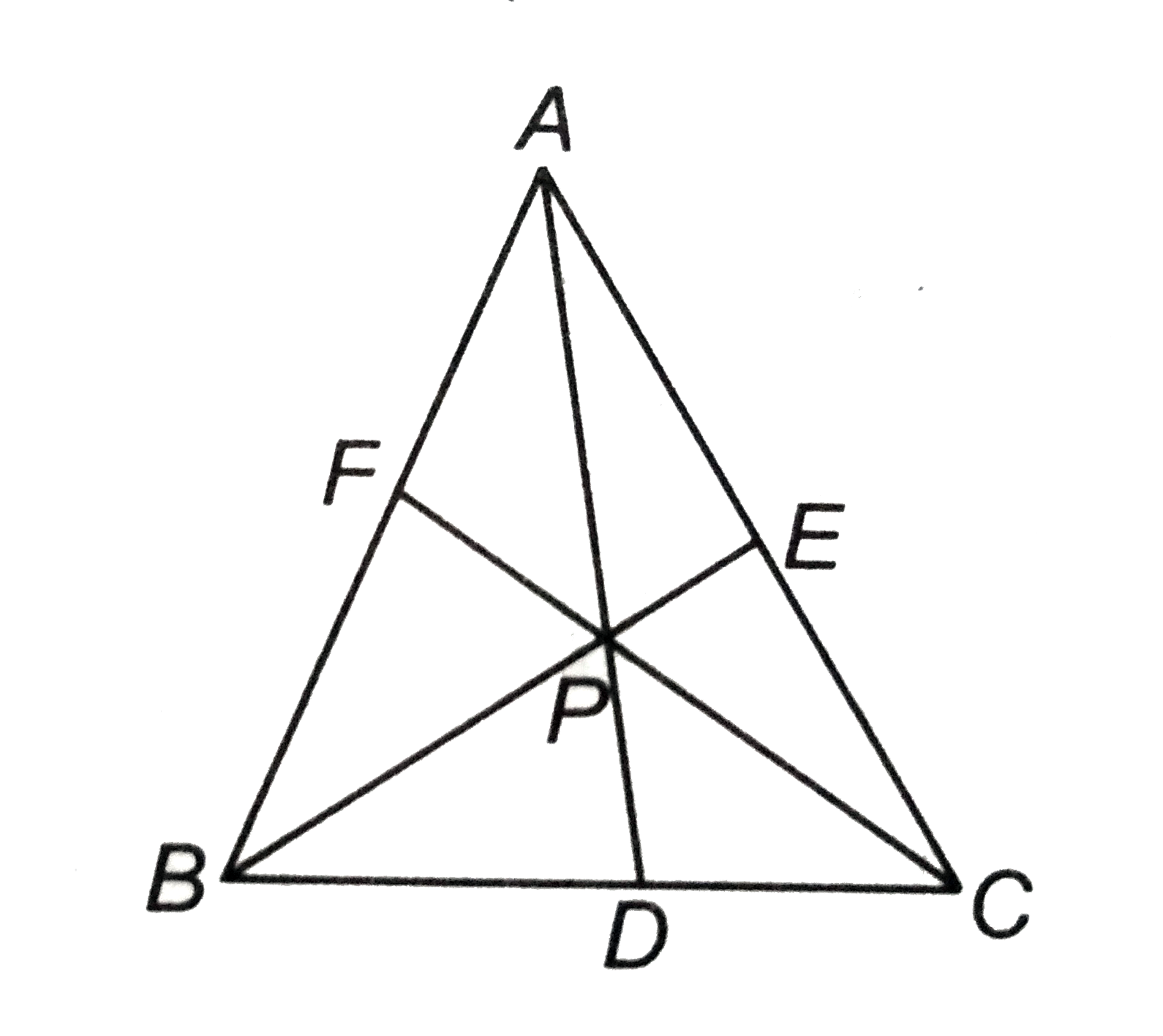
मान लीजिए A(4, 2), B(6, 5) और C(1, 4) एक त्रिभुज ABC के शीर्ष हैं ।
(i) A से होकर जाने वाली माध्यिका BC से D पर मिलती है । बिंदु D के निर्देशांक ज्ञात कीजिए ।
(ii) AD पर स्थित ऐसे बिंदु P के निर्देशांक ज्ञात कीजिए की AP : PD = 2 : 1 हो ।
(iii) माध्यिकाओ BE और CF पर ऐसे बिन्दुओ Q और R के निर्देशांक ज्ञात कीजिए की BQ : QE = 2 : 1 हो और CR : RF = 2 : 1 हो ।
(iv) आप क्या देखते हैं ?
[नोट : वः बिंदु जो तीनो मध्यिकाओ में सर्वनिष्ठ हो, उस त्रिभुज का केन्द्रक (centroid) कहलाता है और यह प्रत्येक माध्यिका को 2 : 1 के अनुपात में विभाजित करता है ।]
(v) यदि A(x1,y1),B(x2,y2) और C(x3,y3) त्रिभुज ABC के शीर्ष हैं, तो इस त्रिभुज के केन्द्रक के निर्देशांक ज्ञात कीजिए ।
A≡(4,2),B≡(6,5),C≡(1,4)
(i) D, BC का मध्य-बिंदु है ।
∴D के निर्देशांक =(6+12,5+42)=(72,92)
(ii) माना P के निर्देशांक = (x, y)
P, AD को 2 : 1 के अनुपात में विभाजित करता है ।
x=2×72+1×42+1
∴ =7+43=113
तथा y=2×92+1×22+1
=9+23=113
∴ बिंदु P के निर्देशांक =(113,113)
(iii) AC के मध्य-बिंदु E के निर्देशांक
=(4+12,2+42)=(52,3)
BE को 2 : 1 के अनुपात में विभाजित करने वाले बिंदु Q के निर्देशांक
=⎛⎝2⋅52+1⋅62+1,2⋅3+1⋅52+1⎞⎠
=(5+63,6+53)=(113,113)
पुन: AB के मध्य-बिंदु F के निर्देशांक
=(4+62,2+52)=(5,72)
CF के 2 : 1 अनुपात में विभाजित करने वाले बिंदु R के निर्देशांक
=⎛⎝2⋅5+1⋅12+1,2⋅72+1⋅42+1⎞⎠
=(10+13,7+43)=(113,113)
(iv) त्रिभुज की मध्यिकाओ का एक संगामी बिंदु है, जो प्रत्येक माधियका को 2 : 1 के अनुपात में विभाजित करता है ।
(v) यदि ΔABC के शीर्ष A(x1,y1),B(x2,y2) तथा C(x3,y3) हैं, तो इस त्रिभुज के केन्द्रक के निर्देशांक
=(x1+x2+x33,y1+y2+y33)
Topper's Solved these Questions
- निर्देशांक ज्यामितिBook:NOOTAN HINDIChapter:निर्देशांक ज्यामितिExercise:अतिलघु उत्तरीय प्रश्न
Explore 10 Videos
- निर्देशांक ज्यामितिBook:NOOTAN HINDIChapter:निर्देशांक ज्यामितिExercise:लघु उत्तरीय प्रश्न
Explore 10 Videos
- निर्देशांक ज्यामितिBook:NOOTAN HINDIChapter:निर्देशांक ज्यामितिExercise:प्रश्नावली 7.3
Explore 5 Videos
- द्विघात समीकरण Book:NOOTAN HINDIChapter:द्विघात समीकरण Exercise:विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
Explore 7 Videos
- पृष्ठीय क्षेत्रफल और आयतन Book:NOOTAN HINDIChapter:पृष्ठीय क्षेत्रफल और आयतन Exercise:बहुविकल्पीय प्रश्न
Explore 7 Videos
Similar Questions
a का मान ज्ञात कीजिए यदि बिंदु (3, a) रेखा 2x - 3y = 5 पर स्थित है ।
View Solutionयदि A(-2, 4) B(0, 0) और C(4, 2) ΔABC, के शीर्ष हैं, तो A से जाने वाली माध्यिका की लम्बाई ज्ञात कीजिए ।
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं :
(i) (2, 3), (-1, 0), (2, -4)
(ii) (-5, -1), (3, -5), (5, 2)
View Solutionनिम्नलिखित प्रश्न में चार विकल्प दिए गए हैं। उस विकल्प को चुनकर अपनी उत्तर पुस्तिका में लिखिए जिसके मूल वास्तविक हैं:
View Solutionएक सुराही निम्नलिखित का संयोजन है :
View Solutionयदि अक्षो को 45∘ से घुमाया जाये तो बिंदु (4,3) के नए निर्देशांक ज्ञात कीजिए ।
View Solutionबिंदु P,Q,R,S के निर्देशांक (2,a),(3,5),(3,4)और (0,6) है । यदि रेखा PR लंबवत हो QS पर तो a का मान ज्ञात कीजिए ।
View Solutionबिंदु A(1,2) से होकर जाने वाली रेखा X-अक्ष के साथ 60∘ का कोण बनाती है तथा x+y=6 को बिंदु P पर काटती है तो AP की लम्बाई ज्ञात कीजिए
View Solutionकिसी वर्ग के विपरीत शीर्षो के निर्देशांक (1,2) तथा (3,8) है , तो शीर्ष (1,2) से होकर जाने वाली रेखाओ तथा विकर्ण का समीकरण ज्ञात कीजिए ।
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionउस बिंदु के निर्देशांक ज्ञात कीजिए जहां बिंदुओं (5 ,1 ,7 ) और ( 3 ,4 ,1 ) को मिलाने वाली रेखा समतल 4x- 3y -z+ 1=0 को काटती है|
View Solutionदिए गये आकृति से बिन्दुओ P, Q, R व S के निर्देशांक ज्ञात कीजिए -
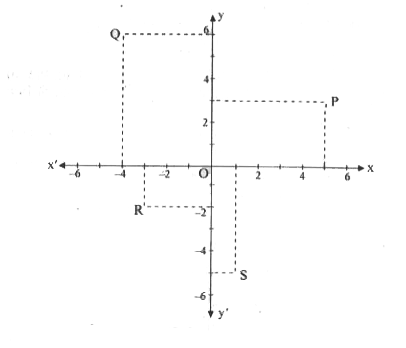
View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
View Solutionतीन बिंदुओं A, B और C के निर्देशांक क्रमश : (3,4),(4,3) एवं (0,3) है । त्रिभुज ABC के परिकेन्द्र के निर्देशांक ज्ञात कीजिए ।
View Solutionबिंदुओं (−3,−1),(−1,3) और (6,2) से बने त्रिभुज के परिकेन्द्र के निर्देशांक ज्ञात कीजिए ।
View Solution

