A long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
μ0i2π(yˆi−xˆj)(x2+y2)
μ0i2π(xˆi+yˆj)(x2+y2)
μ0i2π(xˆj−yˆi)(x2+y2)
μ0i2π(xˆj−yˆi)(x2+y2)
The correct Answer is:A
Magnetic field at P is ¯¯¯B, perpendicular to OP in the direction shown in figure.
So, ¯¯¯B=Bsinθˆi−Bcosθˆj
Here B=μ02πIr
sinθ=yr and cosθ=xr
∴¯¯¯B=μ0I2π1r2(yˆi−xˆj)=μ0I(yˆi−xˆj)2π(x2+y2)

Topper's Solved these Questions
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Exercise-2 PART-2
Explore 26 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Exercise-2 PART-3
Explore 18 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Exercise-1 PART-2
Explore 54 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
Similar Questions
(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)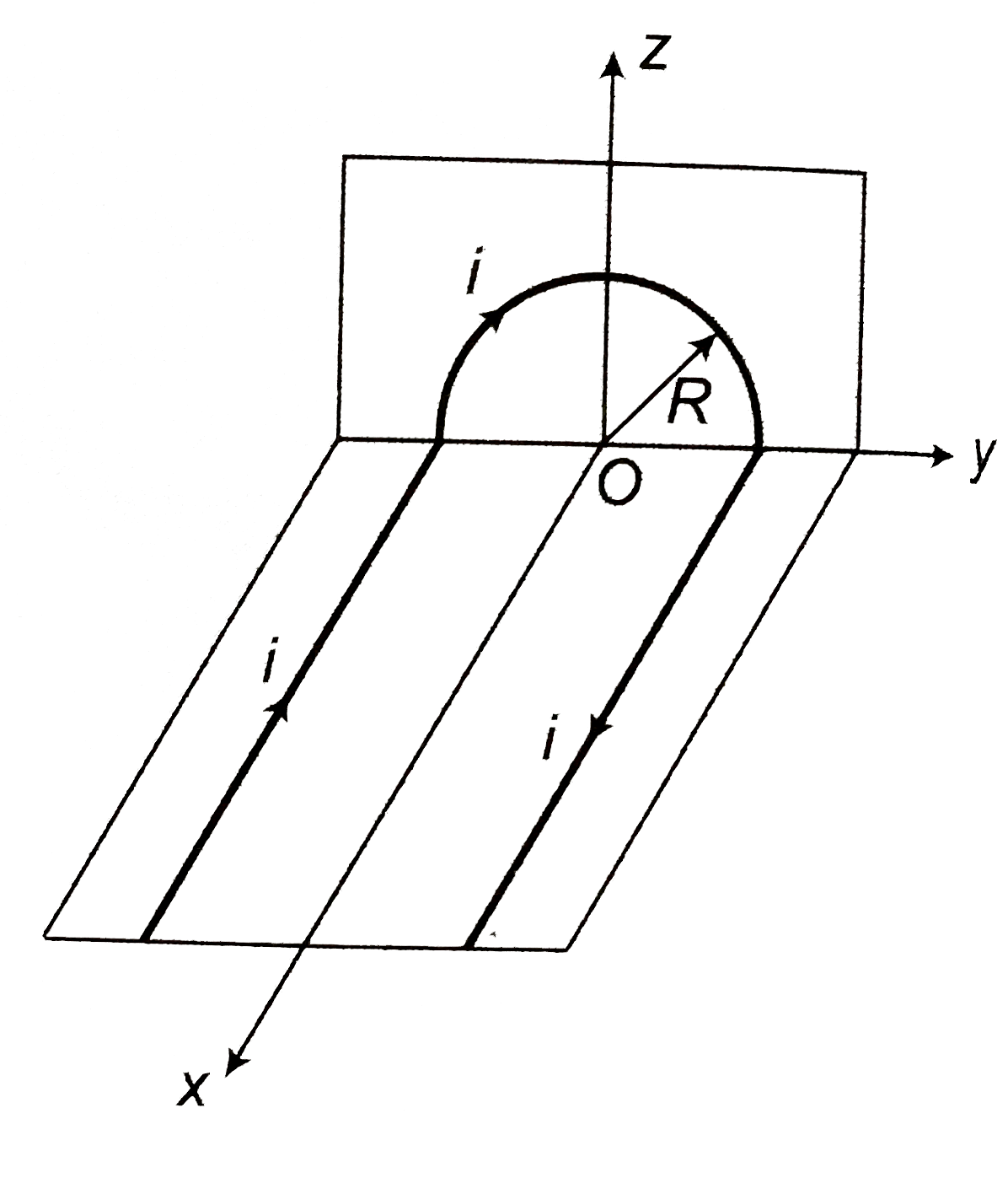
(ii)
(iii)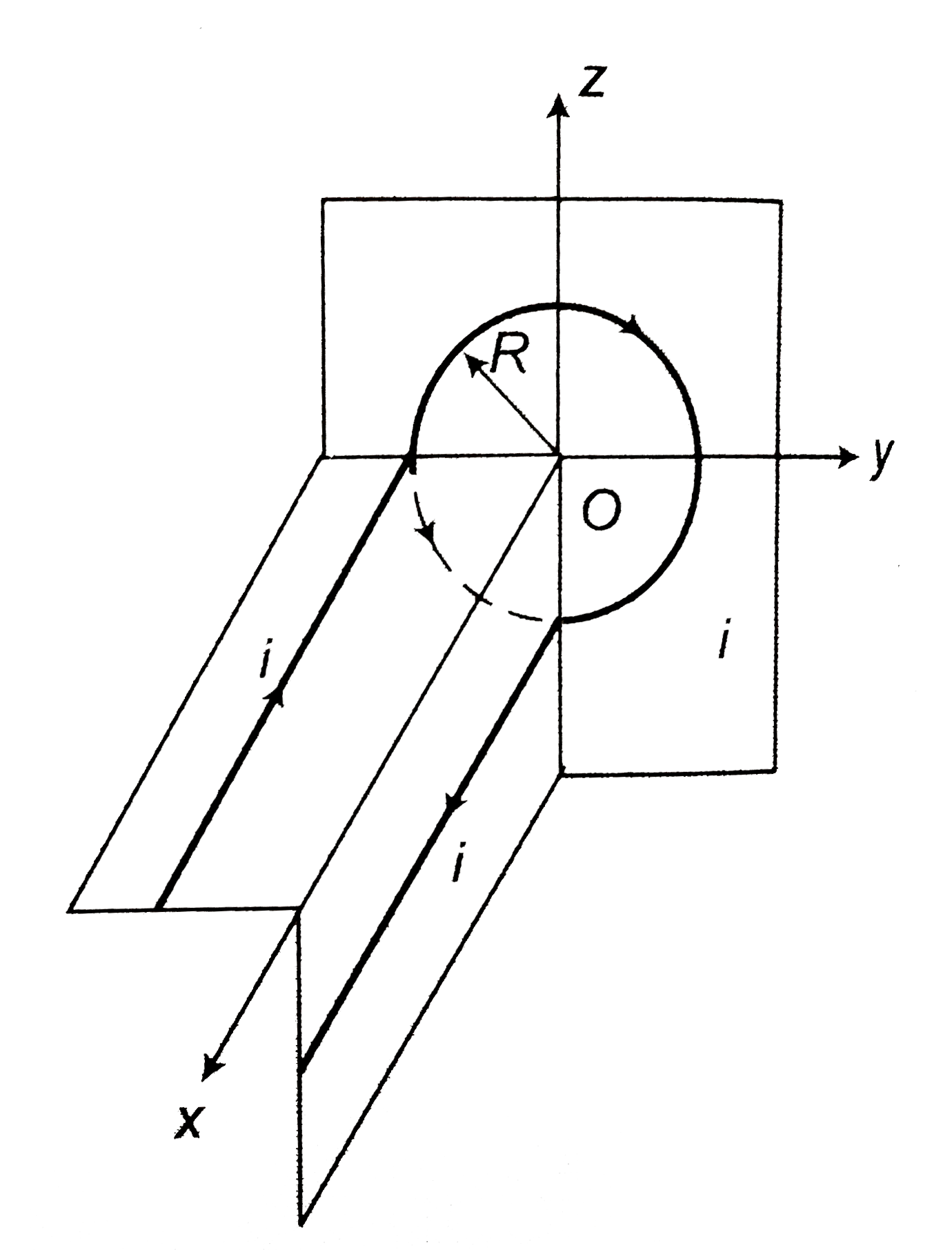
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
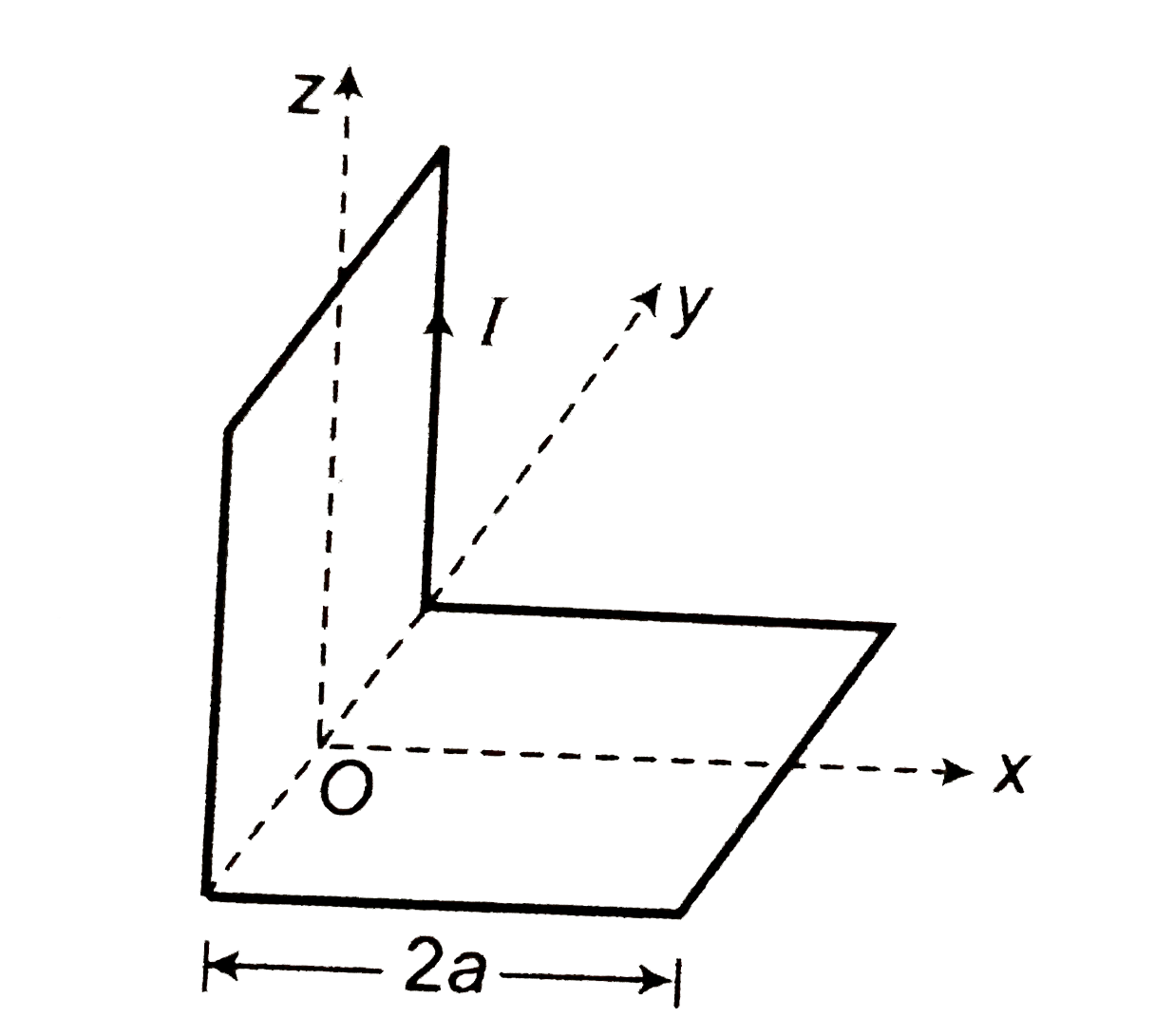
View SolutionA long, straight wire lies along the y-axis and carries a current I=8A in the y-direction (as shown in Fig) In addition to the magnetic field due to the current in the wire, a uniform magnetic field →B0 with magnitude 1.50×10−6T is in the +x direction. What is the total field (magnitude and direction ) at following points in the plane?
(a)x=0,z=1.00m
(b) x=1.00m,z=0
(c) x=0,z=−0.25m

View Solution
Knowledge Check
A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+Y2)Bμ0I(xˆi+yˆj)2π(x2+Y2)Cμ0I(xˆj−yˆi)2π(x2+Y2)Dμ0I(xˆi−yˆj)2π(x2+Y2)A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+y2)Bμ0I(xˆi+yˆj)2π(x2+y2)Cμ0I(xˆj−yˆi)2π(x2+y2)Dμ0I(xˆi−yˆj)2π(x2+y2)A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coordinate (x,y) on the z=0 plane is:
Aμ0I(yˆi−xˆj)2π(x2+y2)Bμ0I(xˆi+yˆj)2π(x2+y2)Cμ0I(xˆj−yˆi)2π(x2+y2)Dμ0I(xˆi−yˆj)2π(x2+y2)
A long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionA long conducting wire of radius 1 cm carrying current of 1 A placed with its axis coinciding with X-axis. Find the magnetic field at point having coordinates (0.5cm,0.5cm) .
View SolutionAn infinitely long, noc-conducting cylidner of radius R lies along the z-axis. Five long, conducting wires are parallel to the cylinder and spaced equally on the upperhalf of its surface. Each wire carries a current I in the opposite z-direction. Find the magnetic field on the z-axis. opposite z-direction. Find the magnetic field on the z-axis.
View SolutionA long straight wire in the horizontal plane carries as curret of 75 A in north to south direction, magnitude and direction of field B at a point 3 m east of the wire is
View Solution

