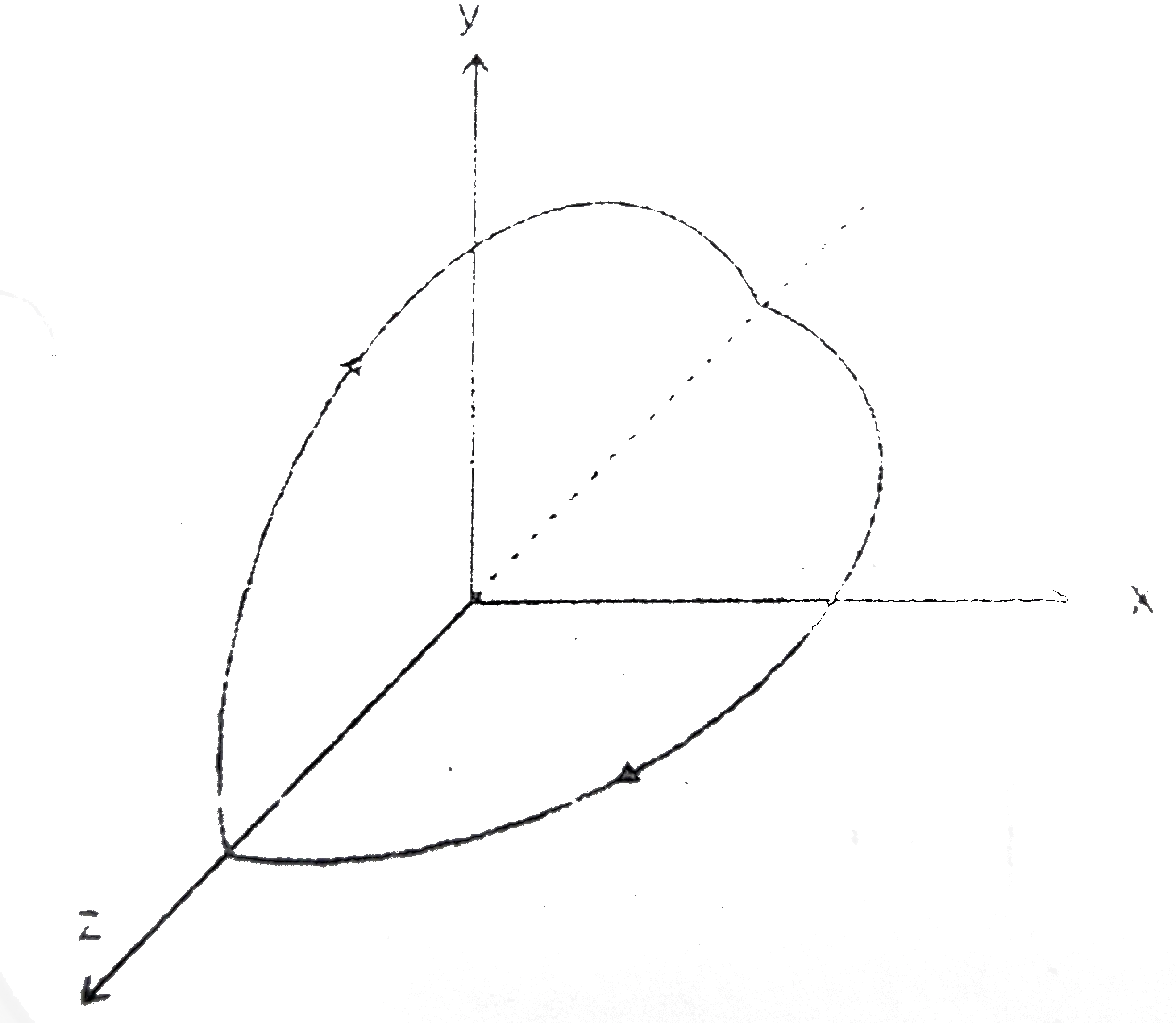
A non-planar circular loop consists of two semi-circles one of which lies in yz-plane & the other is in xz-plane as shown.The magnetic force experienced by positive charge of value Q moving with velocity v along x direction when it is at the origin is:
Qvμ0I4R
Qvμ0I2R
Qvμ0I2√2R
0
The correct Answer is:A
F=q(→V×→B)=Q[vˆi×[μ0I4πR(ˆi+ˆj)]]=Qv.μ0I4πR(ˆk).
Topper's Solved these Questions
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Exercise-2 PART-2
Explore 26 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Exercise-2 PART-3
Explore 18 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Exercise-1 PART-2
Explore 54 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
Similar Questions
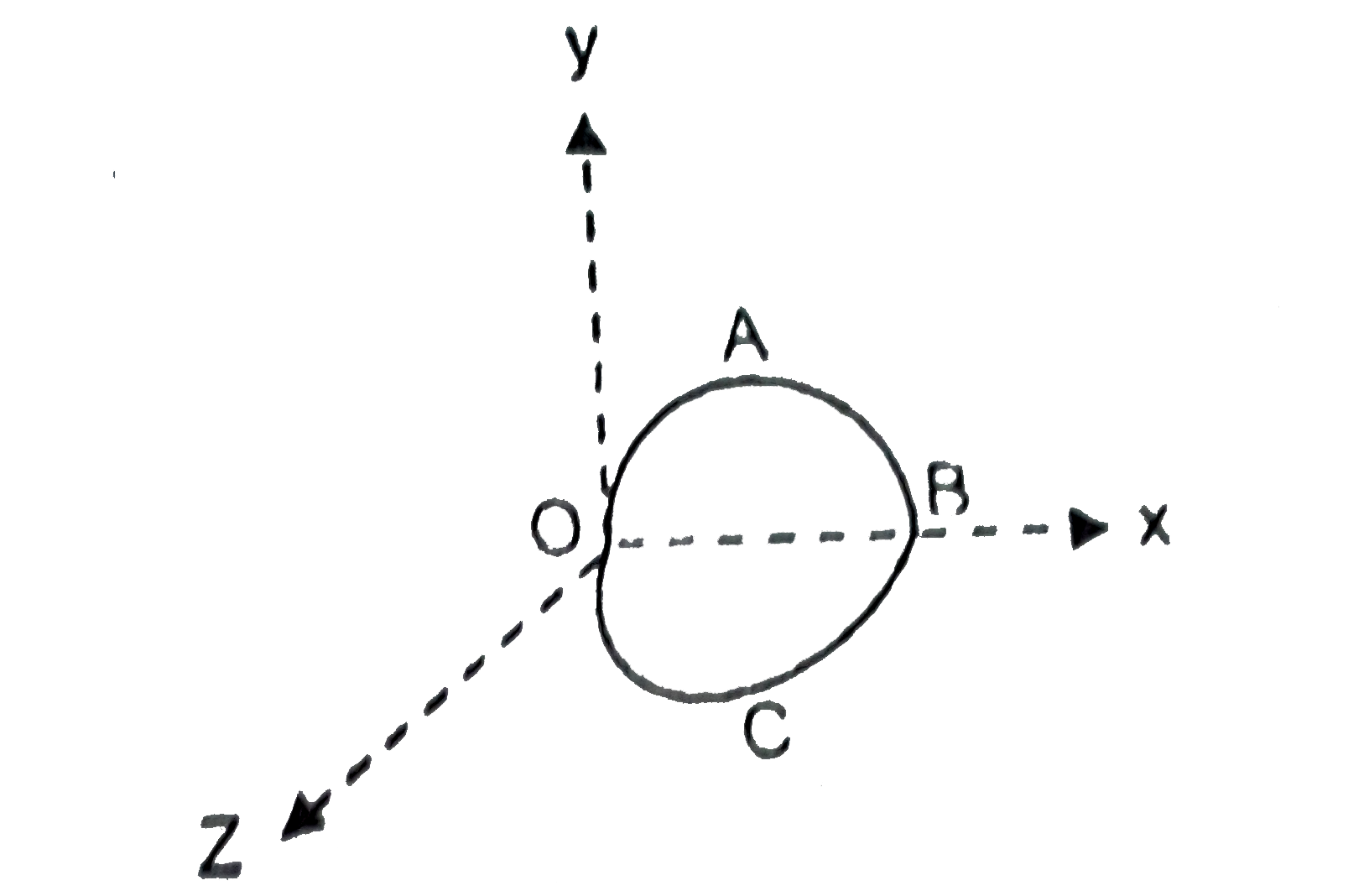
A circular loop is bent so that half of (OAB) lies in xy- plane ane the other half (OCB) lie in xz-plane. A time varying magnetic field axis here given by B=α(tˆj−2tˆk) where α is a positive constant. What will be the direction of induced current.
View SolutionA circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of 30,A the se micircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at origin. Current I is flowing through each of the semicircles as shown in figure.
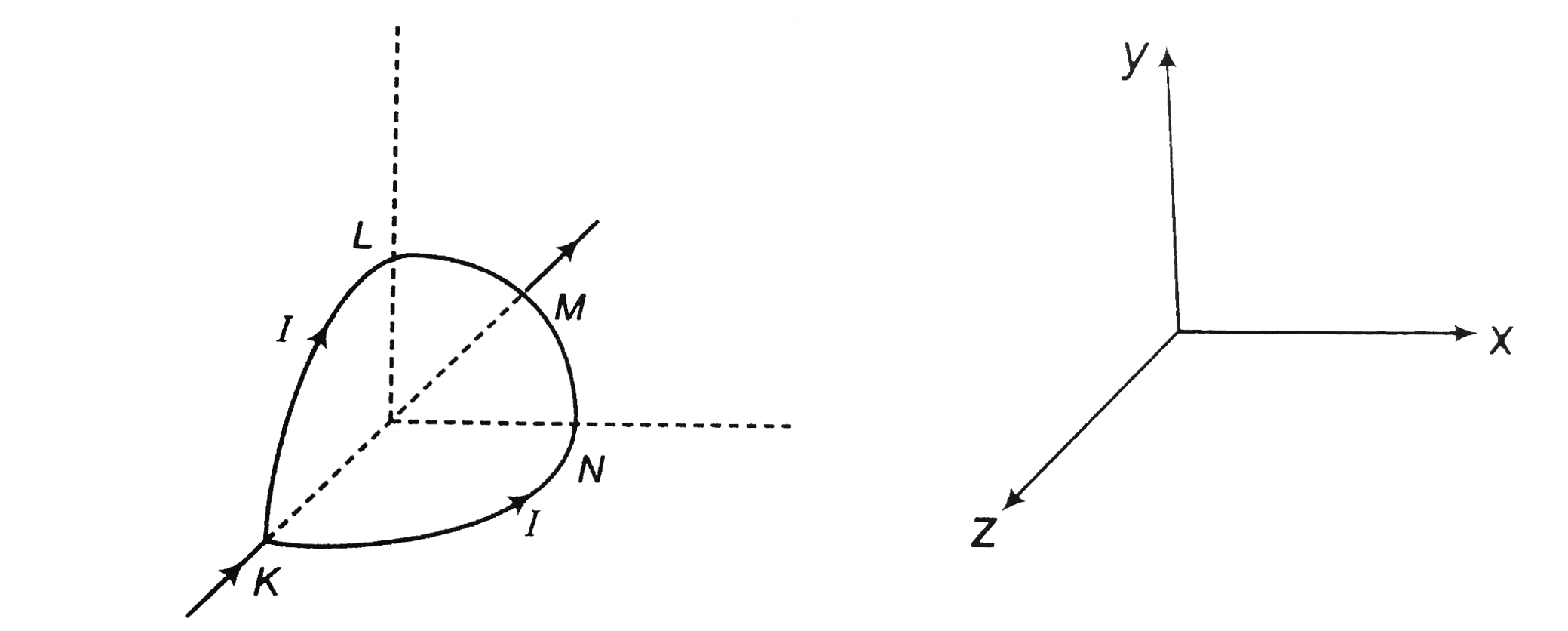
(a) A particle of charge q is released at the origin with a velocity v=−v0ˆi. Find the instantaneous force F on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied, determine the force F1 and F2 on the semicircles KLM and KNM due to the field and the net force F on the loop.
View Solution
Knowledge Check
A 3D structure of current carrying wire is as shown in the figure.
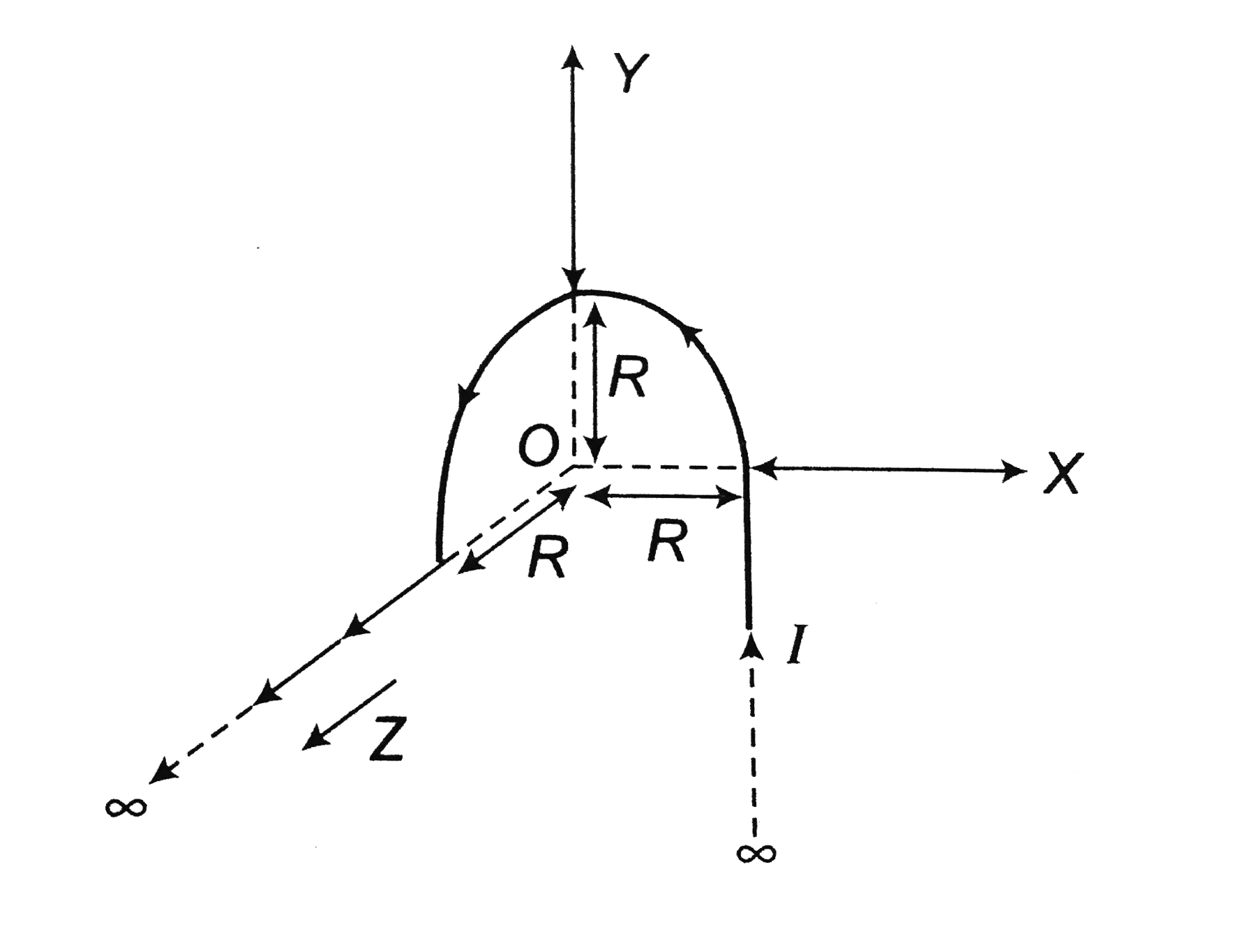
The magnetic force experienced by a charge particle of mass m and charge q, when it is crossing origin with velocity →v along positive Y-axis will beA(μ0Iqv8R+μ0Iqv4πR)ˆiBμ0Iqv8R[(1+2π)ˆi−ˆk]C−μ0Iqv8ˆkDzeroTwo positive charges q1andq2 are moving with velocities v1andv2 when they are at points A and B, respectively, as shown in Fig. The magnetic force experienced by charge q1 due to the other charge q2 is
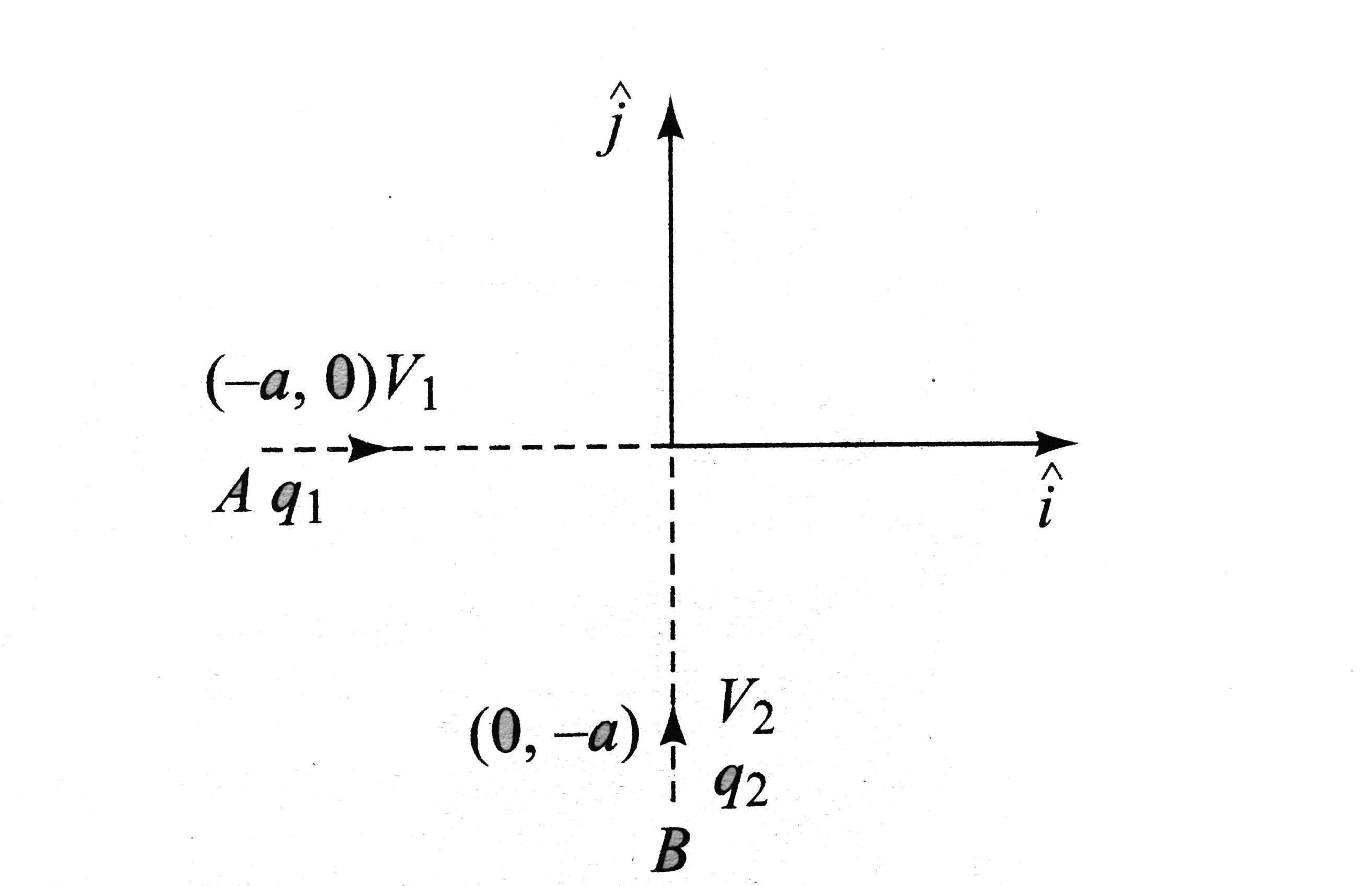 Aμ0q1q2v1v28√2πa2Bμ0q1q2v1v24√2πa2Cμ0q1q2v1v22√2πa2Dμ0q1q2v1v2√2πa2
Aμ0q1q2v1v28√2πa2Bμ0q1q2v1v24√2πa2Cμ0q1q2v1v22√2πa2Dμ0q1q2v1v2√2πa2A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-y plane. If the current in the loop is i, the resultant magnetic field due to two semicircular parts at their common centre is
Aμ0i2√2RBμ0i2RCμ0i4RDμ0i√2R
A ring carrying current l lies in x-z plane as shown. A short magnetic dipole with dipole moment directed along x-axis is fixed at origin. If the ring is free to move anywhere, then it will

View Solution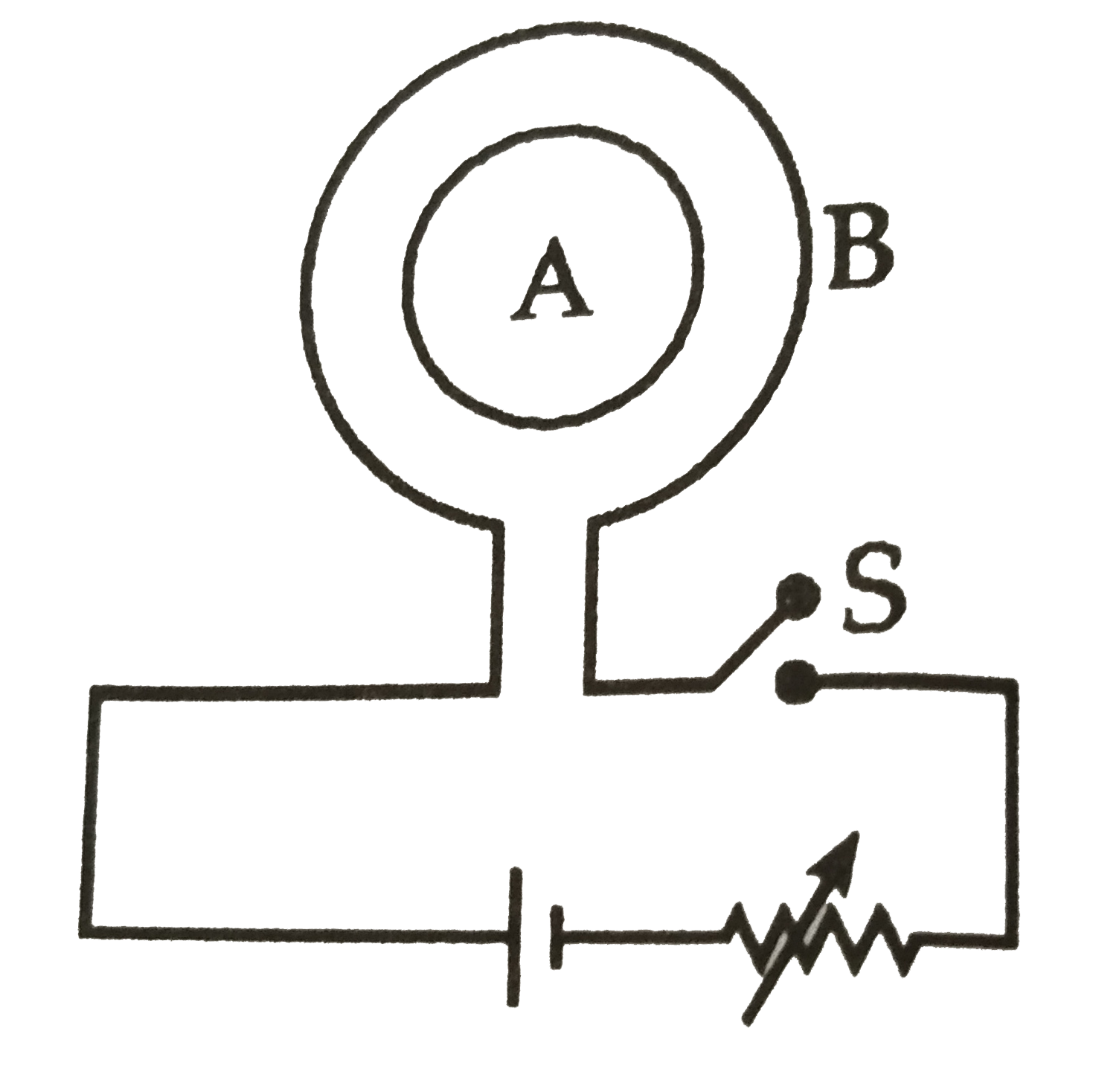
A closed circular wire loop A lies in the plane of longer loop B, which is connected to the battery as shown in the figure. The direction of current induced in the loop A when the switch S is closed is
View SolutionA current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. If the current in the loop is i. The resultant magnetic field due to the two semicircular parts at their common centre is
View SolutionIn Fig ABCDEFA was a square loop of side l, but is folded in two equal parts so that half of it lies in the x-z plane and the other half lies in the y-z plane. The origin O is centre of the frame also. The loop carries current 'i'. The magnetic field at the centre is

View SolutionEight charges each of value q each are placed on a ring of radius R placed in x-y plane with origin at centre -q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v. The velocity of -q when it reaches the centre of ring is (neglect gravity)-

View Solution