Question

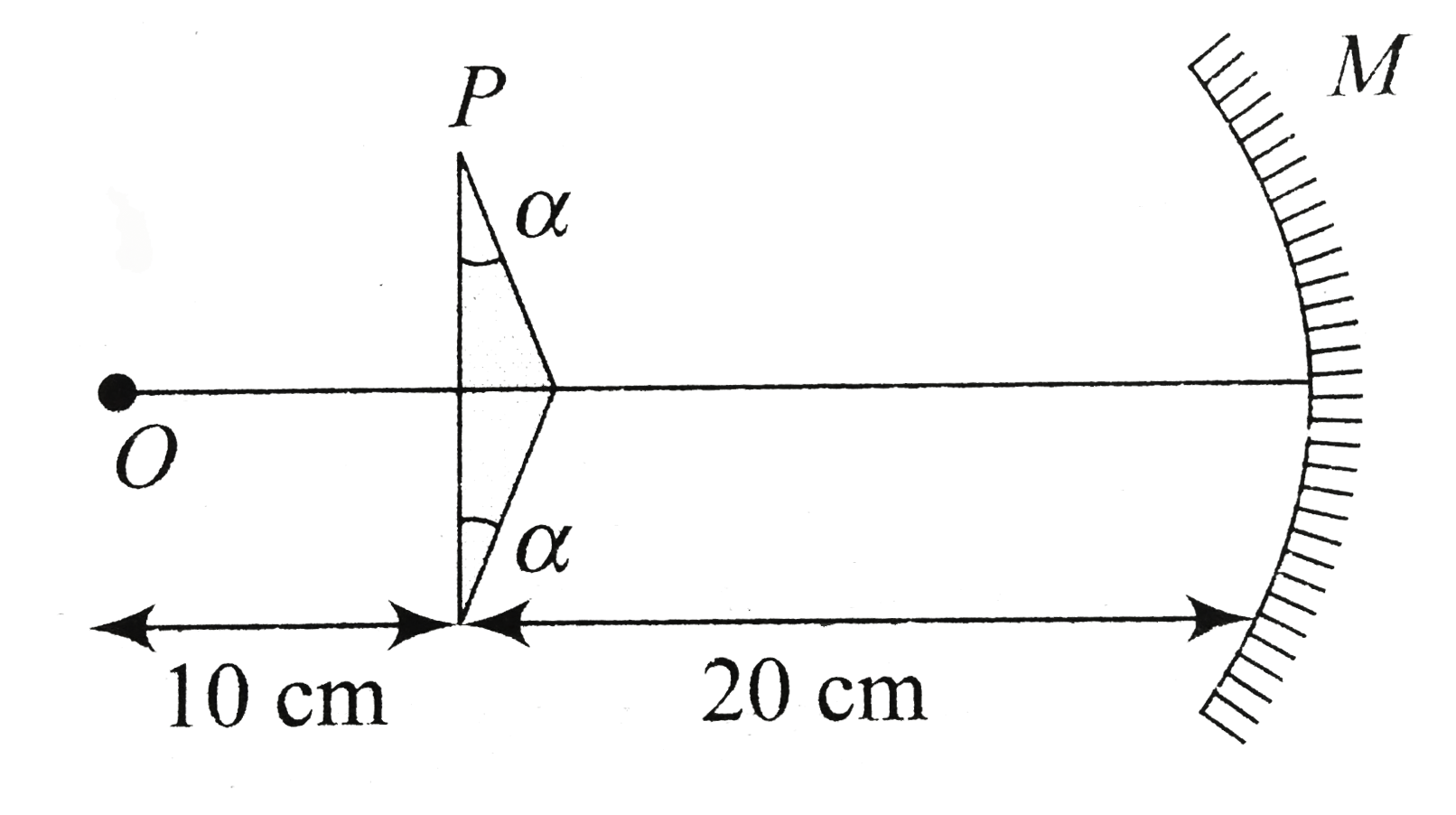
In the given figure, ${\displaystyle O}$ is a point object kept on the principal axis of a concave mirror ${\displaystyle M}$ of radius of curvature ${\displaystyle 20cm}$. ${\displaystyle P}$ is a prism of angle ${\displaystyle \alpha ={1.8}^{\circ }}$. Light falling on the prism (at small angle of incidence) get refracted through the prism and then fall on the mirror. Rrfractive index of prism is ${\displaystyle 3/2}$. Find the distance between the images formed by the concave mirror due to this light.

Answer

`(pi)/(20) cm`.

Explanation

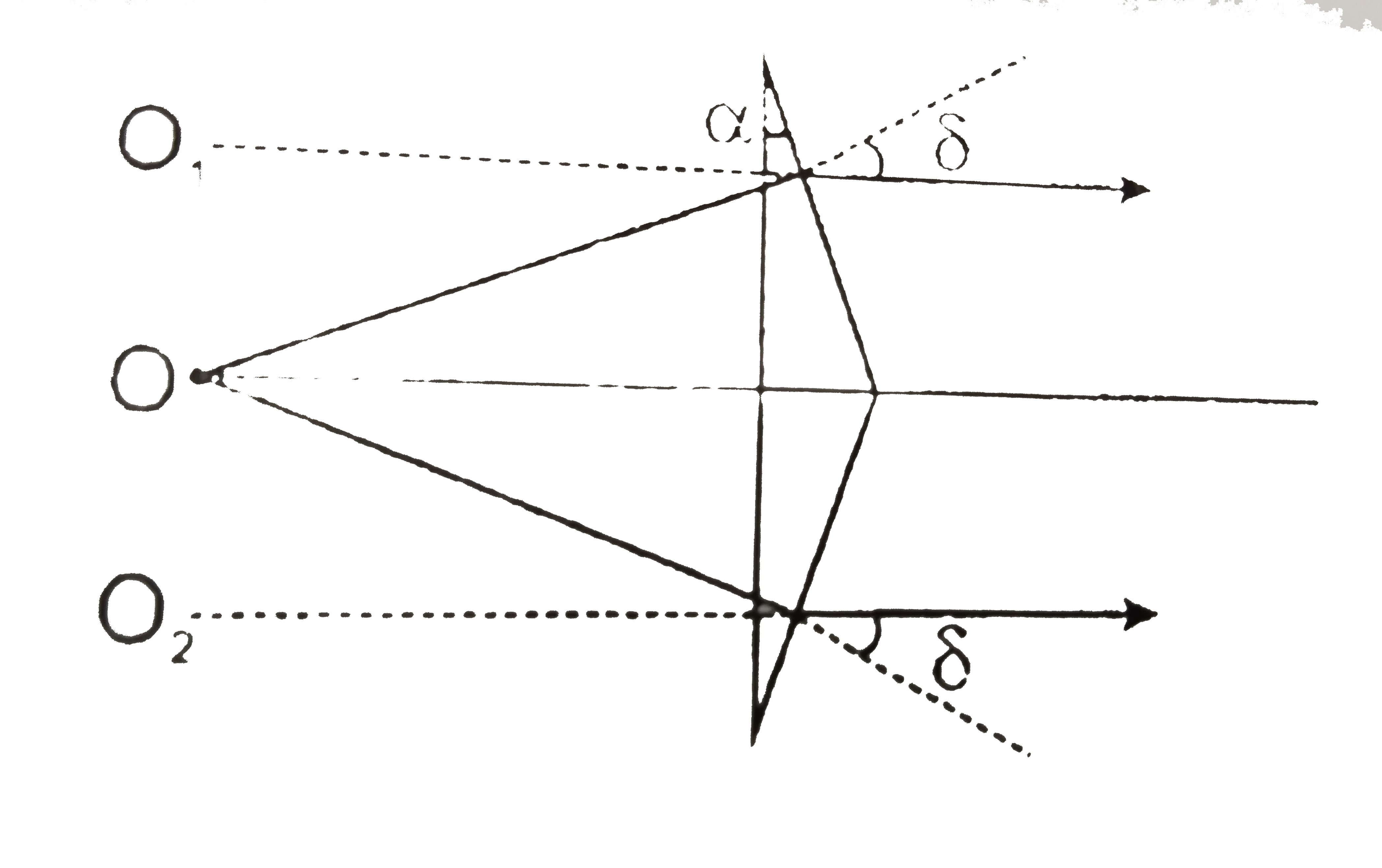
For thin prism `delta=(mu-1)alpha`
`=(1.5-1)1.8^(@)=(0.5)1.8^(@)xx(pi)/(180)rad=(pi)/(200)rad `
`therefore` Distance `OO_(1)=10xx(pi)/(200)=(pi)/(20) cm`
similarly distance `OO_(2)=(pi)/(20)cm`
For mirror `O_(1),O_(2)` are two point objects, at a distance of `30 cm`.
Now applying mirror formula
`(1)/(v)+(1)/(-30)=(1)/(-10)`
`therefore v=-15 cm`
Lateral magnification
`=-(v)/(u)=(-(15))/(30)=-(1)/(2)`
(-ve sign indicates inverted image)
`therefore If `O_(1)` and `O_(2)` are the images formed, then distance between then
`O_(1)'O'_(2)` =(1)/(2)O_(1)O_(2)=(1)/(2).(pi)/(10)=(pi)/(20)cm.