Focal length of a thin lens in air, is 10 cm. Now medium on one side of the lens is replaced by a medium of refractive index $μ = 2$ . The radius of curvature of surface of leng, in contact with the medium, is 20 cm. Find the point on principal axis where parallel rays incident on lens from air parallel to axis will converge.
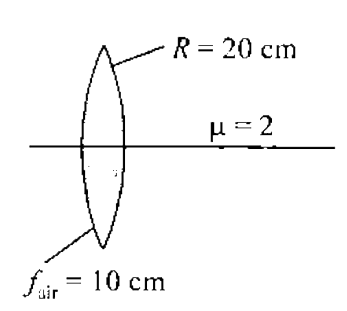
$Focal length of a thin lens in air, is 10 cm. Now medium on one side of the lens is replaced by a medium of refractive index mu = 2. The radius of curvature of surface of leng, in contact with the medium, is 20 cm. Find the point on principal axis where parallel rays incident on lens from air parallel to axis will converge.$

Video Solution

Text Solution

Verified by Experts

Let radius of $1$ surface be $R_{1}$ and refreactive index of lens be $μ$ . Let parallel rays be incident on the lens. Appyling refractiion formula at first surface
$\frac{μ}{v_{1}} - \frac{1}{\infty = \frac{μ - 1}{R_{1}} ... . . (1)}$
At $I I$ surface $\frac{2}{v} - \frac{μ}{v_{1}} = \frac{2 - μ}{- 20} ... . (2)$
Adding (1) and (2)
$\frac{μ}{v_{1}} - \frac{1}{\infty} + \frac{2}{v} - \frac{μ}{v_{1}} = \frac{μ - 1}{R (1)} + \frac{2 - μ}{- 20}$
$= (μ - 1) (\frac{1}{R_{1}} - \frac{1}{- 20}) = \frac{μ - 1}{20} - \frac{2 - μ}{20} = \frac{1}{f}$ (in air) $+ \frac{1}{20} - \frac{2}{20}$
$\Rightarrow v = 40 c m \Rightarrow f = 40 c m$

Updated on:21/07/2023