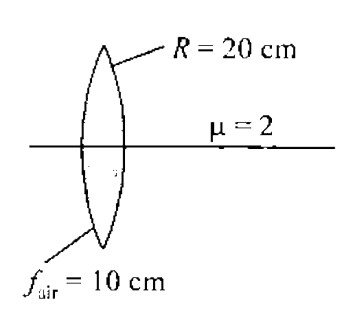
Focal length of a thin lens in air is 10cm. Now, medium on one side of the lens is replaced by a medium of refractive inidex μ=2. The radius of curvature of the surface of lens, in contact with the medium, is 20cm. Find the new focal length.
Let radius of surface I and R1 and refractive index of the lens be μ. Let parallel rays be incident on the lens.
Applying refraction formula at the first surface,
μV1−1∞=μ−1R1 (i)
At the second surface 2V=μV1=2−μ−20 (ii)
Addinig (i) and (ii), we get
μV1−1∞+2VμV1−μ−1R1+2−μ−20=(μ−1)
(1R1−1−20)−μ−120−2−μ20=1f( in air )+120−220
⇒v=40cm⇒f=40cm

Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Solved Examples
Explore 15 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.1
Explore 14 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
Focal length of a thin lens in air, is 10 cm. Now medium on one side of the lens is replaced by a medium of refractive index μ=2. The radius of curvature of surface of leng, in contact with the medium, is 20 cm. Find the point on principal axis where parallel rays incident on lens from air parallel to axis will converge.
View SolutionA planocovex lens is made of a material of refractive in μ=1.5 The radius of curvature of curved surface of the lens is 20.cm. If its plane surface3 is silvered, the focal length of the silvered lens will be
View Solution
Knowledge Check
A planoconvex lens is made of refractive index 1.6. The radius of curvature of curved surface is 60 cm. The focal length of the lens is
A50 cmB100 cmC200 cmD400 cmA plano-convex lens is made of refractive index 1.6. The radius of curvature of the curved surface is 60 cm. The focal length of the lens is
A200 cmB100 cmC50 cmD400 cmThe radius of curvature of each surface of a lens is 40 cm. Its refractive index is 1.5. The focal length of lens will be
A40 cmB20 cmC80 cmD30 cm
A plano-convex lens is made of material having refractive index 1.5. The radius of curvature of curved surface is 60 cm. The focal length of the lens is ______ cm.
View SolutionA plano-convex lens is made of glass of refractive index 1.6. the radius of curvature of its curved surface is 30 cm. What is the focal length of the lens ?
View SolutionFocal length of convex lens in air is 16 cm (μglass=1.5). Now the lens is submerged in liquid of refractive index 1.42. Find the ratio of focal length in medium to focal length in air has closest value
View SolutionA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
View SolutionThe focal length of a biconvex lens is 20 cm and its refractive index is 1.5. If the radii of curvatures of two surfaces of lens are in the ratio 1:2, then the larger radius of curvature is (in cm)
View Solution