What should be the value of refractive index n of a glass rod placed in air, so that the light entering through the flat surface of the rod does not cross the curved surface of the rod?
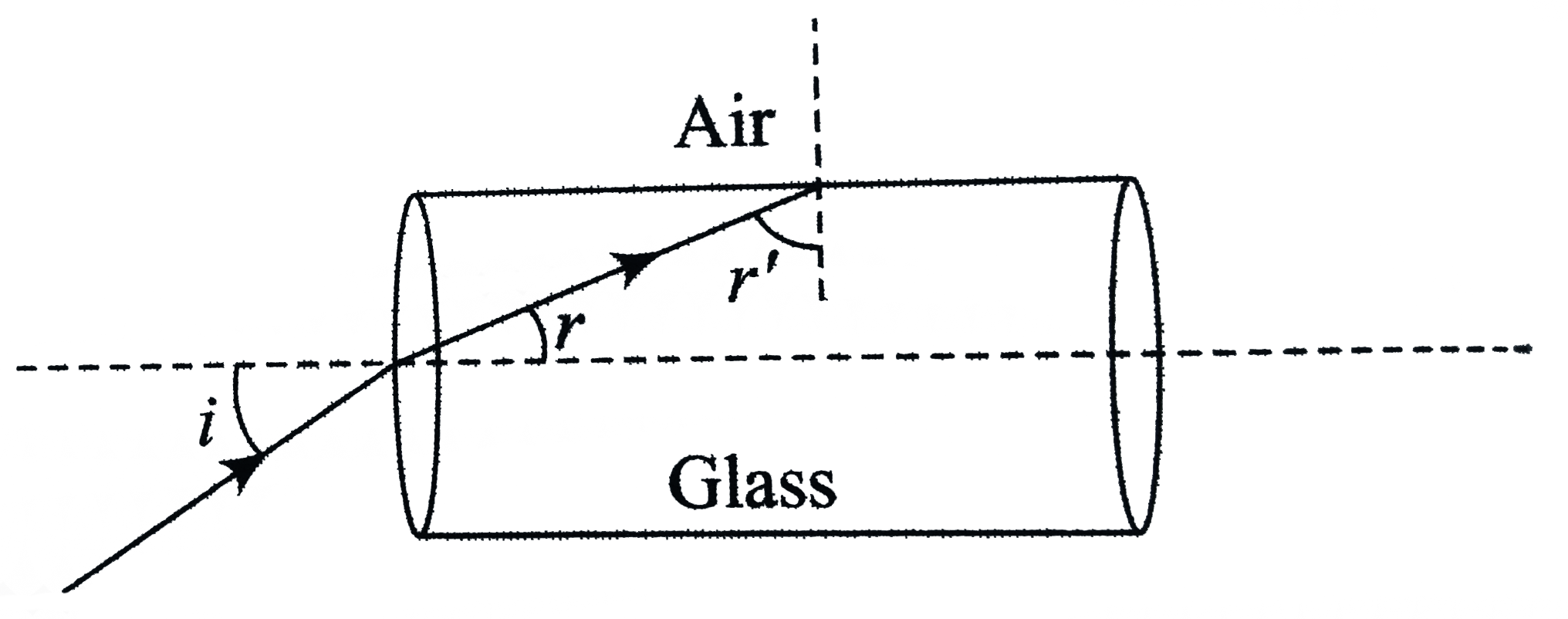
It is required that all possible r' should be more than critical angle. This will be automatically fulfilled if minimum r' is more than critical angle
Angle r' is minimum when r is maximum i.e C (why ?) Therefore the minimum value of r' is 90−C
From condition (A):
90∘−C>C or C<45∘
sinC<sin45∘,1n<1√2 or n>√2

Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Problem
Explore 33 Videos
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Exercise-1
Explore 142 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCEChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
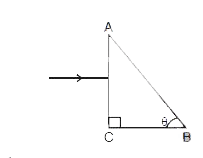
What should be the value of angle θ so that light entering normally through the surface AC of a prism (n=3/2) does not cross the second refracting surface AB?

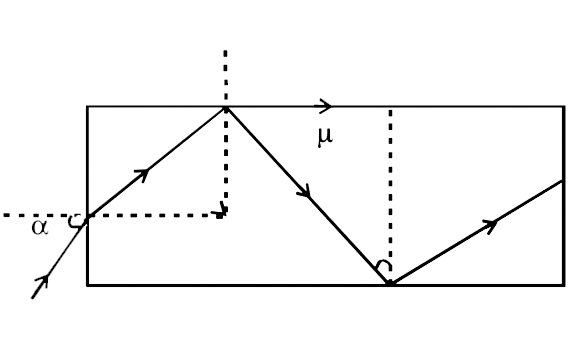
View SolutionLight is incident at an angle i on one planer end of a transparent cylinderical rod of refractive index μ. Find the least value of μ so that the light entering the rod does not emerge from the curved surface of the rod irrespective of the value of i.

View Solution
Knowledge Check
Light enters at an angle of incidance in a tranjsparent road of refractve index μ. for what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidance ?
Aμ>√2Bμ=1Cμ=1.1Dμ=1.3An image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
A20 cmB40 cmC30 cmD50 cmA point source of light is placed at a depth of h below the surface of water of refractive index μ.A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface . The minimum diameter of the disc is
A2h(μ2−1)12B2h(μ2−1)12Ch2(μ2−1)12Dh(μ2−1)12
What should be the value of angle so that light entering normally through the surface AC of a prism (n = 3/2) does not cross the second refracting surface AB.
View SolutionLight is incident at an angle α on one planar end of a transparent cylindrical rod of refractive index μ. Determine the least value of μ so that the light entering the rod does not emerge from the curved surface of rod irrespective of the value of α
View SolutionA point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
View SolutionLight enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence.
View SolutionLight enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence.
View Solution
