What should be the value of angle so that light entering normally through the surface AC of a prism (n = 3/2) does not cross the second refracting surface AB.
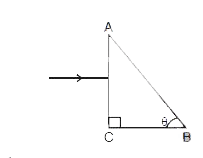
Light ray will pass the surface AC without bending since it is incident normally. Suppose it strikes the surface AB at an angle of incidence i.
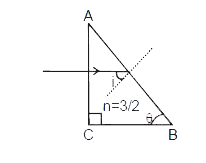
i=90∘−θ
For the required condition :
90∘−θ>C
or sin(90∘−θ)>sinC
or cosθ>sinC
=13/2=23
or θ<cos−123
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:MOTIONChapter:GEOMETRICAL OPTICSExercise:Exercise - 1 Section A - Plane Mirror
Explore 12 Videos
- GEOMETRICAL OPTICSBook:MOTIONChapter:GEOMETRICAL OPTICSExercise:Exercise - 1 Section B, C, D, E - Mirror formula and Magnification, Velocity in Spherical Mirror, Cutting of Mirrors, Combination of Mirrors, Intensity of light
Explore 10 Videos
- FLUIDBook:MOTIONChapter:FLUIDExercise:Exercise-4 level-II
Explore 5 Videos
- GRAVITATIONBook:MOTIONChapter:GRAVITATIONExercise:Exercise - 4 Section - B Previous Years Problems
Explore 15 Videos
Similar Questions
What should be the value of angle θ so that light entering normally through the surface AC of a prism (n=3/2) does not cross the second refracting surface AB?

View SolutionWhat should be the value of refractive index n of a glass rod placed in air, so that the light entering through the flat surface of the rod does not cross the curved surface of the rod?
View Solution
Knowledge Check
A monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
A35∘B39∘C42∘D44∘A monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
AA<2CBA = 2CCA>2CDA<C2In figure, ABC is the cross section of a right-angled prism and ACDE is the cross section of a gless slab. The value of θ so that light incident normally on the face AB does not cross the face AC is (given sin−1(3/5)=37∘).
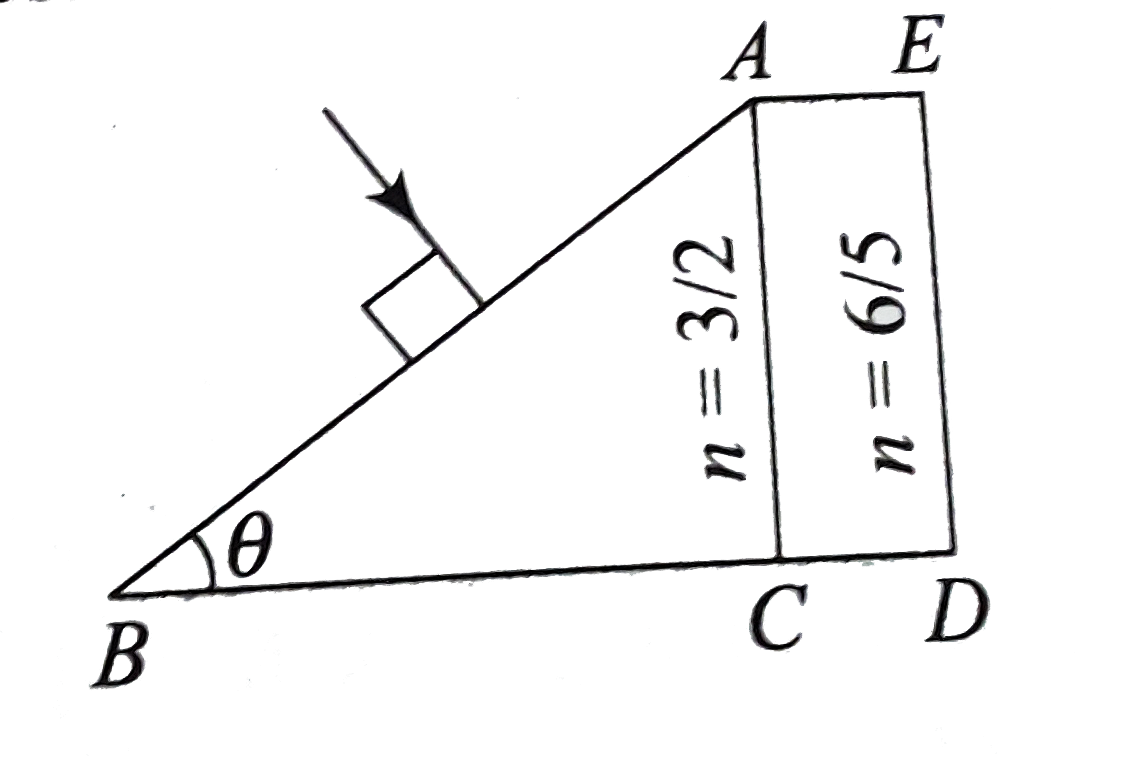 Aθ≤37∘Bθ<37∘Cθ≤53∘Dθ<53∘
Aθ≤37∘Bθ<37∘Cθ≤53∘Dθ<53∘
A ray of light is incident normally on one of the refracting surfaces of a prism of refracting angle A,. The emergent ray grazes the other refracting surface. Find the refractive index of the material ofprism.
View SolutionIn the figure ABC is the cross-section of a right angled prism and BCDE is the cross-section of a glass slab. The value of theta so that light incident normally on the face AB does not cross the face BC is (Givensin−13/5=37∘)

View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
View SolutionA ray of light is incident normally on one of the refracting surfaces of a prism of refracting angle A,. The emergent ray grazes the other refracting surface. Find the refractive index of the material ofprism.
View SolutionWhat angle does a normal make with the opaque surface?
View Solution