A string vibrates in 4 segments to a frequency of 400 Hz.
(a) What is its fundamental frequency?
(b) What frequency will cause it to vibrate into 7 segments?
The correct Answer is:(a) 100Hz , (b) 700Hz
(a) 
2λ=l
4f0=400⇒f0=100Hz
(b) 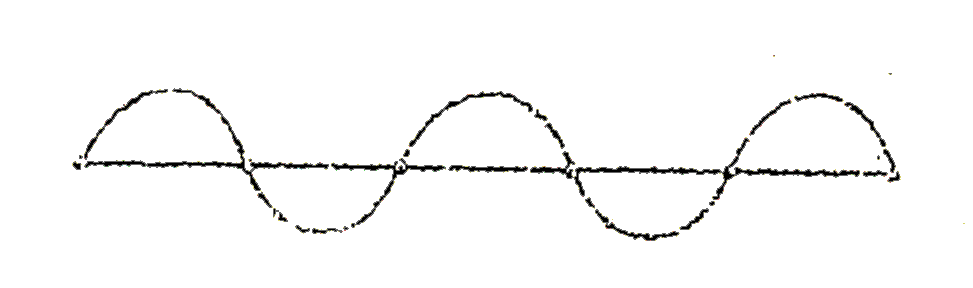
7λ2=λ⇒λ=2l7
vf=2l7∴f=7v2l=700Hz
Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART II
31 Videos
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART I
21 Videos
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Board Level Exercise
27 Videos
- TRAVELLING WAVESBOOK - RESONANCECHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART II
7 Videos
- WAVE OPTICSBOOK - RESONANCECHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
A violin string vibrates with fundamental frequency of 510 Hz. What is the frequency of first overtone? ( Ans: n1 = 1020 Hz )
View SolutionA string vibrating with a fundamental frequency of 8 Hz has tension T1. This string vibrates with a fundamental frequency of 15 Hz when the tension is T2 .
Find the fundamental frequency of the string when its tension is T1+T2 .
View Solution
Knowledge Check
A string vibrates in 5 segments to a frequency of 480 Hz. The frequency that will cause it to vibrate in 2 segments will be
A96 HzB192 HzC1200 HzD2400 HzThe fundamental frequency of a vibrating organ pipe is 200Hz
AThe first overtone may be 400HzBThe first overtone is 400HzCThe first overtone may be 600HzDThe second overtone may be 600HzA wire under a tension vibrates with fundamental frequency of 256 Hz . What should be the fundamental frequency of the wire if its length is half, thickness twice and one - fourth of the tension ?
A128 HzB64 HzC200 HzD96 Hz
The fundamental frequency of an open organ pipe is 512 Hz. What will be its fundamental frequency if its one end is closed ?
View SolutionThe fundamental frequency of a vibrating organ pipe is 200 Hz.
View SolutionIn law of length , the fundamental frequency of vibrating string is
View SolutionIn law of tension, the fundamental frequency of vibrating string is
View SolutionIf the vibrating length of a string is increased by 25%, then its fundamental frequency will
View Solution
