A nylon guiter string has a linear density of 7.20g/m and is under a tension of 150N. The fixed supports are distance D=90.0cm apart. The string is osillating in the stading wave pattern shown in figure. Calculate the (a) speed. (b) wavelength and (c) frequency of the travelling waves whose superposition gives this standing wave. ltbgt 
The correct Answer is:(a) 250√3m/s; , (b) 60.0cm; , (c) 12503√3Hz
Step by step video, text & image solution for A nylon guiter string has a linear density of 7.20 g//m and is under a tension of 150 N. The fixed supports are distance D = 90.0 cm apart. The string is osillating in the stading wave pattern shown in figure. Calculate the (a) speed. (b) wavelength and (c) frequency of the travelling waves whose superposition gives this standing wave. ltbgt by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART II
31 Videos
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART I
21 Videos
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Board Level Exercise
27 Videos
- TRAVELLING WAVESBOOK - RESONANCECHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART II
7 Videos
- WAVE OPTICSBOOK - RESONANCECHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
A nylon guitar string has a linear density of 7.20 g/m and is under a tension of 180 N. The fixed supports are distance D =90.0 cm apart. The string is oscillating in the standing wave pattern shown in Fig. 16-42. Calculate the (a) speed, (b) wavelength, and (c) frequency of the traveling waves whose superposition gives this standing wave.

View SolutionA string has linear density μ=525g/m and is under tension τ=45N. We send a sinusoidal wave with frequency f=120Hz and amplitude ym=8.5 mm along the string. At what average rate does the wave transport energy?
View Solution
Knowledge Check
The velocity of waves in a string fixed at both ends is 2 m / s . The string forms standing waves with nodes 5.0 cm apart. The frequency of vibration of the string in Hz is
A40B30C20D10The displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
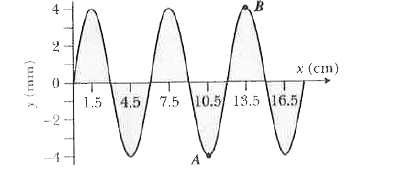
What is the wavelength of the wave?A3.0 cmB6.0 cmC9.0 cmD12 cm
A steel wire 70cm long has a mass of 7.0g. If the wire is under a tension of 100N, what is the speed of transverse waves in the wire?
View SolutionA tuning fork of frequency 440 Hz is attached to a long string of linear mass density 0.01kgm−1 kept under a tension of 49 N. The fork produces transverse waves of amplitude 0.50 mm on the string. (a) Find the wave speed and the wavelength of the waves. (b) Find the maximum speed and acceleration of a particle of the string. (c) At what average rate is the tuning fork transmitting energy to the string ?
View SolutionA string fixed at both ends is 7.50 m long and has a mass of 0.120 kg. It is subjected to a tension of 96.0 N and set oscillating (a) What is the speed of the waves on the string? (b) What is thc longest possible wavelength for a standing wave? (c) Give the frequency of that wave.
View SolutionA string fixed at both ends is 8.40m long and has a mass of 0.120kg. It is subjected to a tension of 96.0N and set oscillating. (a) What is the speed of the waves on the string? (b) What is the longest possible wavelength for a standing wave ? (c) Give the frequency of the wave.
View SolutionTransverse waves travel with a speed of 20.0m/sin a string under a tension of 6.00 N. what tension is requared for a wave speed of 30.0m/s in the same string?
View SolutionIn fig. 16-47a, string 1 has a linear density of 3.00 g/m, and string 2 has a linear density of 5.00 g/m. They are under tension due to the hanging block of mass M= 800 g. Calculate the wave speed on (a) string 1 and (b) string 2 (Hint: When a string loops halfway around a pulley, it pulls on the pulley witii a net force that is twice the tension in the string) Next the block is divided into two blocks (with M1+M2=M) and the apparatus in tearranged as shown in fig. 16-47b. Find (c) M1and(d)M2 such that the wave speeds in the two strings are equal.

View Solution
