Question

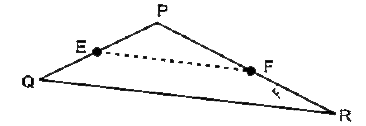
E and F are points on the sides PQ and PR respectively of $\Delta PQR$. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm. EQ = 3 cm. PF = 3.6 cm and FR = 2.4
(ii) PE = 4 cm. QE = 4.5 cm. PF = S cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

Explanation

To determine whether the line segment EF is parallel to QR in each case, we can use the Basic Proportionality Theorem (also known as Thales' theorem). According to this theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.

The theorem states that if EF || QR, then:

$$\frac{PE}{EQ}=\frac{PF}{FR}$$

We will check this for each case provided.

Case (i):
Given:
- PE = 3.9 cm
- EQ = 3 cm
- PF = 3.6 cm
- FR = 2.4 cm

Step 1: Calculate the ratios.

1. Calculate \( \frac{PE}{EQ} \):
\( \frac{PE}{EQ} = \frac{3.9}{3} = 1.3 \)

2. Calculate \( \frac{PF}{FR} \):
\( \frac{PF}{FR} = \frac{3.6}{2.4} = 1.5 \)

Step 2: Compare the ratios.

Since \( 1.3 \neq 1.5 \), we conclude that EF is not parallel to QR.

Conclusion for Case (i):
EF is not parallel to QR.

---

Case (ii):
Given:
- PE = 4 cm
- EQ = 4.5 cm
- PF = 5 cm
- RF = 9 cm

Step 1: Calculate the ratios.

1. Calculate \( \frac{PE}{EQ} \):
\( \frac{PE}{EQ} = \frac{4}{4.5} = \frac{8}{9} \)

2. Calculate \( \frac{PF}{RF} \):
\( \frac{PF}{RF} = \frac{5}{9} \)

Step 2: Compare the ratios.

Since \( \frac{8}{9} \neq \frac{5}{9} \), we conclude that EF is not parallel to QR.

Conclusion for Case (ii):
EF is not parallel to QR.

---

Case (iii):
Given:
- PQ = 1.28 cm
- PR = 2.56 cm
- PE = 0.18 cm
- PF = 0.36 cm

Step 1: Calculate the ratios.

1. Calculate \( \frac{PE}{PQ} \):
\( \frac{PE}{PQ} = \frac{0.18}{1.28} \)

2. Calculate \( \frac{PF}{PR} \):
\( \frac{PF}{PR} = \frac{0.36}{2.56} \)

Step 2: Simplify the ratios.

1. For \( \frac{0.18}{1.28} \):
\( \frac{0.18 \times 100}{1.28 \times 100} = \frac{18}{128} = \frac{9}{64} \)

2. For \( \frac{0.36}{2.56} \):
\( \frac{0.36 \times 100}{2.56 \times 100} = \frac{36}{256} = \frac{9}{64} \)

Step 3: Compare the ratios.

Since \( \frac{9}{64} = \frac{9}{64} \), we conclude that EF is parallel to QR.

Conclusion for Case (iii):
EF is parallel to QR.

---

Summary of Results:
- Case (i): EF is not parallel to QR.
- Case (ii): EF is not parallel to QR.
- Case (iii): EF is parallel to QR.