In right angled ΔABC,∠B=90∘andAB=√34 units . The co-ordinares of points B, C are (4. 2) and (-1, y) respectively . If ar ΔABC=17 sq . Units, then find the value of y .
The correct Answer is:y=−1,y=5
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the given information
We have a right-angled triangle ABC with:
- Angle B = 90 degrees
- Length of AB = √34 units
- Coordinates of B = (4, 2)
- Coordinates of C = (-1, y)
- Area of triangle ABC = 17 square units
Step 2: Use the area formula for a triangle
The area of a triangle can be calculated using the formula:
Area=12×base×height
In this case, we can take BC as the base and AB as the height. Therefore, we can write:
12×BC×AB=17
Substituting the value of AB:
12×BC×√34=17
Step 3: Solve for BC
Multiplying both sides by 2:
BC×√34=34
Now, divide both sides by √34:
BC=34√34=√34
Step 4: Find the length of BC using the distance formula
The distance formula between two points (x1,y1) and (x2,y2) is given by:
d=√(x2−x1)2+(y2−y1)2
Applying this to points B (4, 2) and C (-1, y):
BC=√((−1)−4)2+(y−2)2
This simplifies to:
BC=√(−5)2+(y−2)2=√25+(y−2)2
Step 5: Set the two expressions for BC equal
Now we have two expressions for BC:
√25+(y−2)2=√34
Squaring both sides:
25+(y−2)2=34
Step 6: Solve for y
Subtract 25 from both sides:
(y−2)2=9
Taking the square root of both sides gives:
y−2=3ory−2=−3
Thus:
1. y−2=3⇒y=5
2. y−2=−3⇒y=−1
Step 7: Conclusion
The possible values for y are:
y=5ory=−1
We have a right-angled triangle ABC with:
- Angle B = 90 degrees
- Length of AB = √34 units
- Coordinates of B = (4, 2)
- Coordinates of C = (-1, y)
- Area of triangle ABC = 17 square units
The area of a triangle can be calculated using the formula:
Area=12×base×height
In this case, we can take BC as the base and AB as the height. Therefore, we can write:
12×BC×AB=17
Substituting the value of AB:
12×BC×√34=17
Multiplying both sides by 2:
BC×√34=34
Now, divide both sides by √34:
BC=34√34=√34
The distance formula between two points (x1,y1) and (x2,y2) is given by:
d=√(x2−x1)2+(y2−y1)2
Applying this to points B (4, 2) and C (-1, y):
BC=√((−1)−4)2+(y−2)2
This simplifies to:
BC=√(−5)2+(y−2)2=√25+(y−2)2
Now we have two expressions for BC:
√25+(y−2)2=√34
Squaring both sides:
25+(y−2)2=34
Subtract 25 from both sides:
(y−2)2=9
Taking the square root of both sides gives:
y−2=3ory−2=−3
Thus:
1. y−2=3⇒y=5
2. y−2=−3⇒y=−1
The possible values for y are:
y=5ory=−1
Topper's Solved these Questions
- Co-ordinate GeometryBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - LONG ANSWER TYPE QUESTIONS -III
10 Videos
- Co-ordinate GeometryBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - PRACTICE-TEST (Coordinate Geometry) SECTION-A
4 Videos
- Co-ordinate GeometryBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - VERY SHOT ANSWER TYPE QUESTIONS (State True or False)
22 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE - TEST (SECTION - D)
1 Videos
- CONSTRUCTIONSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CONSTRUCTIONSEXERCISE - (PRACTICE-TEST) SECTION-C
1 Videos
Similar Questions
Knowledge Check
In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
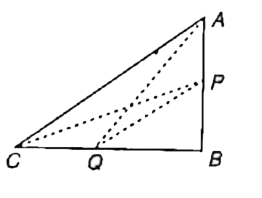 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)The mid-points of AB and AC of a ΔABC are respectively X and Y. If BC + XY = 12 units, then the value of BC - XY is
A6B8C4D12
In ΔABC right angled at C, find the value of cos (A + B).
View SolutionIn a ΔABC,∠A=90∘,∠B=30∘ find the ratio of sides .
View SolutionIn any triangle ABC, if∠C=90∘, AC=4 unit, BC=3, find AB.
View SolutionIf ΔABC is right angled at B then what is the value of sin(A+C)
View SolutionIn a ΔABC,∠B=90∘,AB=7cmand(AC−BC)=1cm, find the values of sinA,cosA,sinCandC.
View SolutionLet A(1, 3), B(0, 0) and C(k, 0) be three points such that ar(△ABC)=3 sq units. Find the value of k.
View Solution
