In any triangle ABC, if∠C=90∘, AC=4 unit, BC=3, find AB.
To solve the problem, we will use the Pythagorean theorem, which applies to right-angled triangles.
1. Identify the Triangle and Given Values:
We have triangle ABC where angle C is 90 degrees. The lengths of the sides are given as:
- AC = 4 units (one leg)
- BC = 3 units (the other leg)
We need to find the length of AB, which is the hypotenuse.
Hint: Remember that in a right triangle, the hypotenuse is opposite the right angle.
2. Apply the Pythagorean Theorem:
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (AB) is equal to the sum of the squares of the lengths of the other two sides (AC and BC). This can be expressed as:
AB2=AC2+BC2
Hint: Make sure to square each side correctly.
3. Substitute the Known Values:
Substitute the values of AC and BC into the equation:
AB2=42+32
Hint: Calculate the squares of the lengths carefully.
4. Calculate the Squares:
Calculate 42 and 32:
42=16and32=9
Now substitute these values back into the equation:
AB2=16+9
Hint: Add the results of the squares together.
5. Perform the Addition:
Now, add the two results:
AB2=25
Hint: This step gives you the square of the hypotenuse.
6. Take the Square Root:
To find AB, take the square root of both sides:
AB=√25
Hint: Remember that the square root of a number gives you the positive value, as lengths cannot be negative.
7. Calculate the Final Value:
Calculate the square root:
AB=5
Hint: This is the final length of the hypotenuse.
Final Answer:
The length of AB is 5 units.
We have triangle ABC where angle C is 90 degrees. The lengths of the sides are given as:
- AC = 4 units (one leg)
- BC = 3 units (the other leg)
We need to find the length of AB, which is the hypotenuse.
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (AB) is equal to the sum of the squares of the lengths of the other two sides (AC and BC). This can be expressed as:
AB2=AC2+BC2
Substitute the values of AC and BC into the equation:
AB2=42+32
Calculate 42 and 32:
42=16and32=9
Now substitute these values back into the equation:
AB2=16+9
Now, add the two results:
AB2=25
To find AB, take the square root of both sides:
AB=√25
Calculate the square root:
AB=5
The length of AB is 5 units.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a right triangle ABC,∠B=90 . If AB=14 cm,BC=48 cm, find AC.
A50B48C20D26
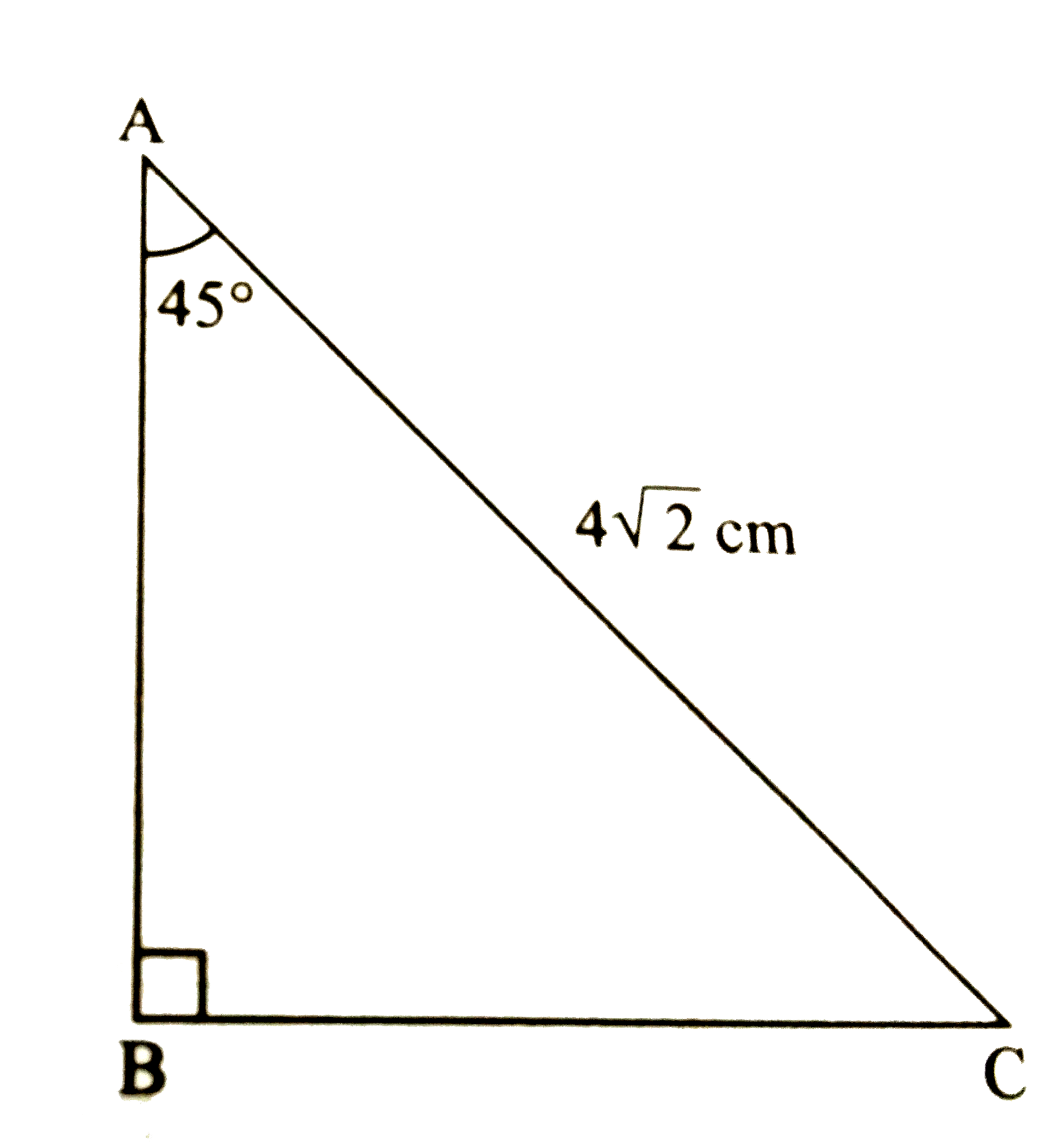
In △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
 View Solution
View SolutionIn a triangle ABC,∠B=90∘,D is the midpoint of AC,BD=√117. Sum of sides of AB & BC is 30 cm. Find the area of triangle ABC.
View SolutionIf in a triangle ABC right angled at B, AB = 6 units and BC = 8 units, then find the value of sin A. cos C + cos A. sin C.
View SolutionConstruct a right-angled triangle ABC in which ∠A=90∘, BC=6cm and AB=4.8cm.
View SolutionIn triangle ABC, A=90∘andAB=3 unit, AC = 4 unit and side AD is perpendicular on BC then find the area of triangle ADB?
View SolutionIn a ΔABC,∠B=90∘,AB=7cmand(AC−BC)=1cm, find the values of sinA,cosA,sinCandC.
View SolutionIf △ABC is a right angled triangle with ∠ABC=90∘, and AC = 10 cm and BC = 8 cm, then the length of AB is:
यदि △ABC एक समकोण त्रिभुज है, ∠ABC=90∘,AC =10, BC =8 cm फिर AB की लंबाई है:View Solution
