When the frequency of AC is doubled, the impedance of an LCR series circuit
is halved
is doubled
increases
decreases
The correct Answer is:C
To solve the problem of how the impedance of an LCR series circuit changes when the frequency of the AC source is doubled, we can follow these steps:
Step 1: Understand the Impedance Formula
The impedance Z of an LCR series circuit is given by the formula:
Z=√R2+(XL−XC)2
where:
- R is the resistance,
- XL=ωL is the inductive reactance,
- XC=1ωC is the capacitive reactance,
- ω=2πf is the angular frequency.
Step 2: Define Initial Impedance
Let’s denote the initial frequency as f. The initial angular frequency is:
ω1=2πf
The initial impedance Z1 can be expressed as:
Z1=√R2+(XL−XC)2=√R2+(ω1L−1ω1C)2
Step 3: Define New Impedance After Doubling Frequency
When the frequency is doubled, the new frequency is 2f, and the new angular frequency is:
ω2=2ω1=4πf
Now, the new impedance Z2 can be expressed as:
Z2=√R2+(X′L−X′C)2
where:
- X′L=ω2L=4πfL
- X′C=1ω2C=14πfC
Thus, we can write:
Z2=√R2+(4ω1L−14ω1C)2
Step 4: Compare the Two Impedances
Now we need to analyze how Z2 compares to Z1:
Z2=√R2+(4ω1L−14ω1C)2
We can see that X′L increases (since it is multiplied by 4), while X′C decreases (since it is divided by 4).
Step 5: Determine the Effect on Impedance
To determine the overall effect on impedance:
- If XL increases significantly more than XC decreases, then Z2 will be greater than Z1.
- Conversely, if XC decreases significantly more than XL increases, then Z2 could be less than Z1.
However, generally, since the inductive reactance increases with frequency and the capacitive reactance decreases, we can conclude that:
Z2>Z1
Conclusion
When the frequency of the AC source is doubled, the impedance Z of the LCR series circuit increases.
---
The impedance Z of an LCR series circuit is given by the formula:
Z=√R2+(XL−XC)2
where:
- R is the resistance,
- XL=ωL is the inductive reactance,
- XC=1ωC is the capacitive reactance,
- ω=2πf is the angular frequency.
Let’s denote the initial frequency as f. The initial angular frequency is:
ω1=2πf
The initial impedance Z1 can be expressed as:
Z1=√R2+(XL−XC)2=√R2+(ω1L−1ω1C)2
When the frequency is doubled, the new frequency is 2f, and the new angular frequency is:
ω2=2ω1=4πf
Now, the new impedance Z2 can be expressed as:
Z2=√R2+(X′L−X′C)2
where:
- X′L=ω2L=4πfL
- X′C=1ω2C=14πfC
Z2=√R2+(4ω1L−14ω1C)2
Now we need to analyze how Z2 compares to Z1:
Z2=√R2+(4ω1L−14ω1C)2
We can see that X′L increases (since it is multiplied by 4), while X′C decreases (since it is divided by 4).
To determine the overall effect on impedance:
- If XL increases significantly more than XC decreases, then Z2 will be greater than Z1.
- Conversely, if XC decreases significantly more than XL increases, then Z2 could be less than Z1.
Z2>Z1
When the frequency of the AC source is doubled, the impedance Z of the LCR series circuit increases.
Topper's Solved these Questions
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - COMPREHENSION(Answer the following questions in view of above passage)
5 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - COMPREHENSION-(II)( Assuming that any resistance of inductor is included in R, answer the following question)
10 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSIGNMENT PROBLEMS(OBJECTIVE Level - Il)
1 Video
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (NUMERICAL BASED QUESTIONS)
4 Videos
Similar Questions
Consider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2))) At parallel circuit resonance, theimpendence is maximum and current is minimum. Parallel resonant circuit is sometimes called the anti-resonance in order to distinguish from series resonance
QFind the impedance of AC circuit at resonance shown in the adjacent figure

Find the impedance of AC circuit at resonance shown in the adjacent figure
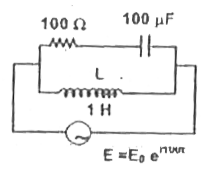
View SolutionThe circuit shown in the figure is a series LCR circuit connected to an AC source. This circuit has many important applications in practical electronic systems. In the given circuit, L=20mH and frequency of applied alternating potential difference is ω=8000rad/s. Initial phase of applied potential difference has such a minimum value that initial value of instantaneous potential difference is half of is peak value while initial phase of current in the circuit has such a minimum value that initial value of instantaneous current equals its peak value. We also observe that current in the circuit leads the net voltage across the circuit. It is given that peak values of potential difference across R and L are I VR(peak))=25V
V(L)peak=20V
Impedance of the circuit is
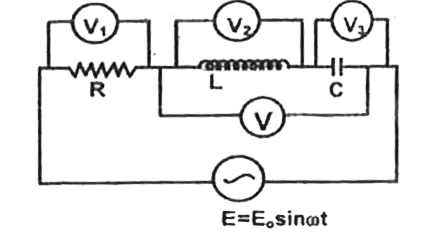
View SolutionIn the given figure, which voltmeter will read zero voltage at resonant frequency omega rad//sec
View SolutionA ball is projected from the floor of a cabin of height 7m with speed 20 m/s at an angle of 37∘ with the floor of cabin. It makes a successive collision with the wall of cabin and then return again to its floor. Assume all collisions are perfectly elastic. Find time taken (in sec) by the ball to reach the floor after collisions with the ceiling of cabin.
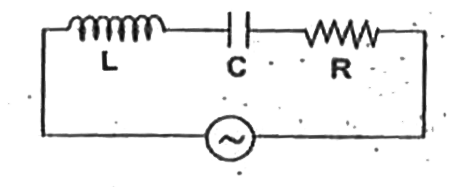
View SolutionIn a series LCR circuit, operated with an ac of angular frequency ω , the total impedance is
View SolutionAt resonance frequency the impedance in series LCR circuit is
View SolutionObtain on expression for impedance and current in series LCR circuit. Deduce an expression for the resonating frequency of an LCR series reasonating circuit.
View SolutionWhen the frequency of AC is doubled, the impedance of an RC circuit is
View SolutionWhen the frequency of AC is doubled, the impedance of an LCR, circuit is
View SolutionSketch graphs to show the variation of (i) current and (ii) impedance of a series LCR circuit with the frequency of the ac source.
View SolutionWhen the frequency of the ac voltage applied to a series LCR circuit is gradually increased from a low value , the impedance of the circuit.
View Solutionउन कारकों का उल्लेख कीजिए जिन पर श्रेणी LCR परिपथ की अनुनादी आवृत्ति निर्भर करती है। श्रेणी LCR परिपथ में आरोपित ac स्रोत की आवृत्ति के साथ प्रतिबाधा में होने वाले परिवर्तन को प्रदर्शित करने वाला ग्राफ खींचिए।
View SolutionDerive an expression for the impedance of a series LCR, circuit, when an AC voltage is applied to it.
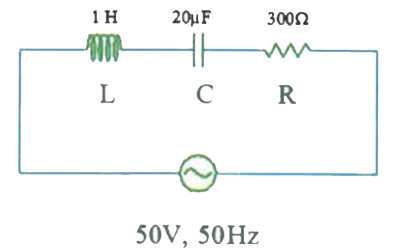
View SolutionIn the series LCR circuit shown, the impedance is
View SolutionFrequency of AC source is continuously increased, impedance of LCR series circuit
View SolutionAt resonance frequency the impedance in series LCR circuit is
View Solution
