The parallel axis theorem can be applied to
any two parallel axes
any two parallel-axes of which one must lie within the body
any two parallel-axes of which one must pass through the centre of mass of the body.
any two parallel axes lying in the plane of the body
The correct Answer is:C
Step by step video, text & image solution for The parallel axis theorem can be applied to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - II
16 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - III
1 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
15 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
Find the moment of inertia of the two uniform joint rods about point P as shown in Fig. Use parallel axis theorem. Mass of each rod is M.
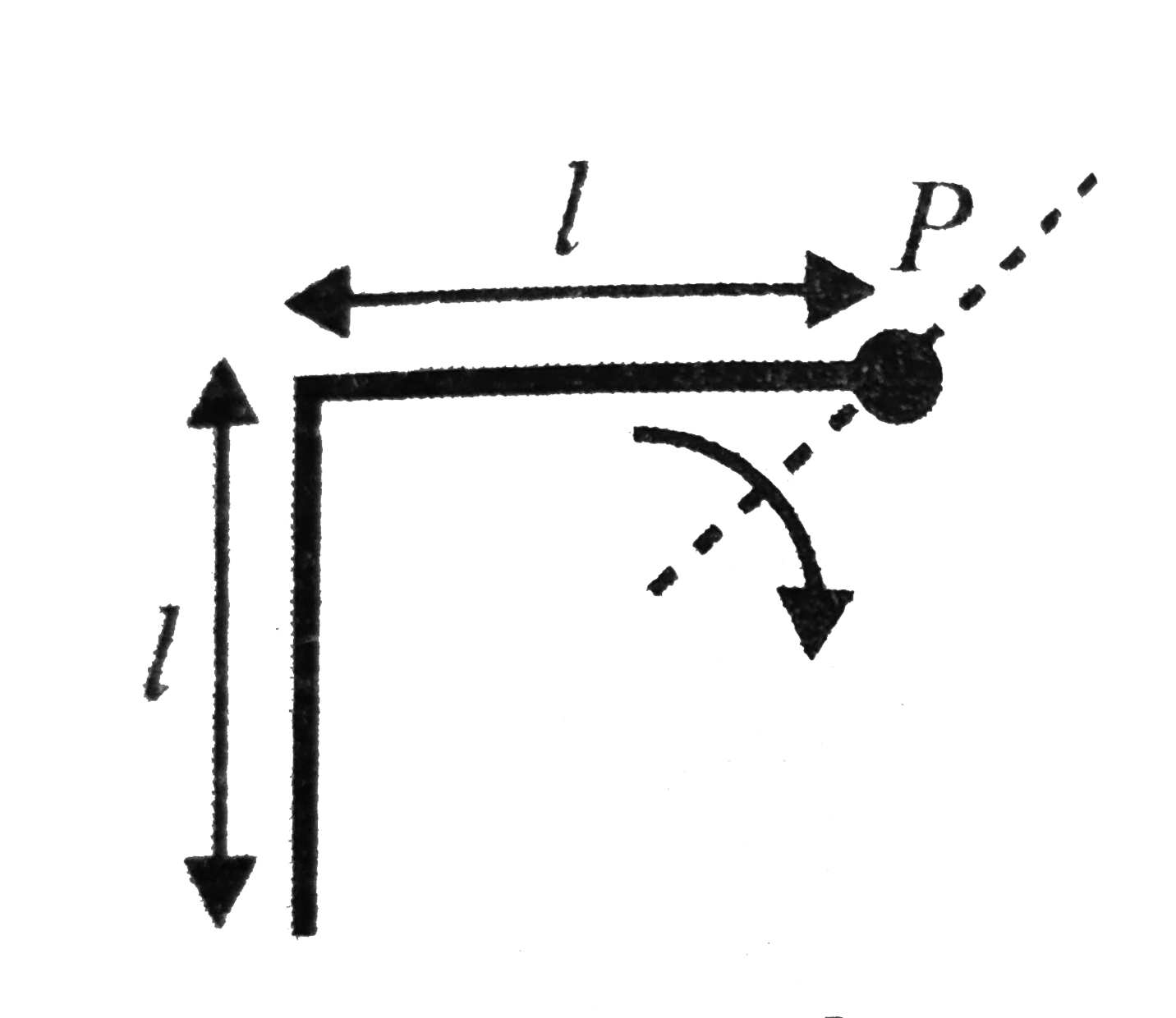
View SolutionUse the parallel axis theorem to find the moment of inertia ofa uniform rod of mass M = 3kg and length 2a (a = 1m), about a perpendicular axis through one end?
View Solution
Knowledge Check
Assertion : Moment of inertia about an axis passing throught centre of mass is always minimum
Reason : Theorem of parallel axis can be applied for 2-D as well as 3-D bodies.AIf both Assertion and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are true but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is fasleDIf Assertion is false but Reason is trueIf Rolle's theorem can be applied to f (x) = xlnx, x>0 in interval [1a,1b] where a,b∈I+ then b equals
A1B2C3Dinfinite possible values existBohr model can be applied on :
AH atomBHe+ionCH−ionDLi2+ion
Using the parallel axes theorem, find the M.I. of a sphere of mass m about an axis that touches it tangentially. Given that Icm=25mr2
View SolutionIf f(x)=xalogxandf(0)=0 then the value of α for which Rolle's theorem can be applied in [0,1] is
View SolutionThe length of longest interval in which Roll's theorem can be applied for the function f(x)=∣∣x2−a2∣∣,(a>0) is:
View SolutionIf f(x)=xalogxandf(0)=0 then the value of α for which Rolle's theorem can be applied in [0,1] is
View SolutionRolle’s theorem can not applicable for :
View Solution
