Three identical solid spheres (1, 2 and 3) are allowed to roll down from three inclined plane of angles θ1,θ2andθ3 respectively starting at time t = 0, where θ1>θ2>θ3, then
sphere 1 will reach the bottom first
sphere 2 will reach the bottom first
sphere 3 will reach the bottom first
all the spheres will reach the bottom at the same time
The correct Answer is:A
To solve the problem of three identical solid spheres rolling down inclined planes with angles θ1,θ2, and θ3 (where θ1>θ2>θ3), we need to analyze the motion of the spheres based on the physics of rolling motion.
1. Identify Forces Acting on the Spheres:
Each sphere experiences gravitational force mg acting downwards. This force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
2. Determine the Acceleration of Each Sphere:
For a solid sphere rolling without slipping, the acceleration a down the incline can be derived from Newton's second law and the rotational motion equations. The net force acting down the incline is mgsinθ, and the moment of inertia I for a solid sphere is 25mr2. The relationship between linear acceleration a and angular acceleration α is given by a=rα.
The equation of motion for the sphere can be written as:
mgsinθ−f=ma
where f is the frictional force.
The torque τ about the center of mass is given by:
τ=Iα=fr
Substituting I and α:
fr=25mr2⋅ar
Simplifying gives:
f=25ma
Substituting f back into the equation of motion:
mgsinθ−25ma=ma
Rearranging gives:
mgsinθ=ma+25ma=75ma
Thus, the acceleration a is:
a=5gsinθ7
3. Compare Accelerations for Each Sphere:
The accelerations of the spheres are given by:
- For sphere 1: a1=5gsinθ17
- For sphere 2: a2=5gsinθ27
- For sphere 3: a3=5gsinθ37
Since θ1>θ2>θ3, it follows that:
sinθ1>sinθ2>sinθ3
Therefore:
a1>a2>a3
4. Conclusion:
The sphere that rolls down the incline with the largest angle θ will have the greatest acceleration and will reach the bottom first. Thus, sphere 1 (with angle θ1) will reach the bottom first, followed by sphere 2, and then sphere 3.
Final Answer:
Sphere 1 will reach the bottom first, followed by sphere 2, and then sphere 3.
Each sphere experiences gravitational force mg acting downwards. This force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
For a solid sphere rolling without slipping, the acceleration a down the incline can be derived from Newton's second law and the rotational motion equations. The net force acting down the incline is mgsinθ, and the moment of inertia I for a solid sphere is 25mr2. The relationship between linear acceleration a and angular acceleration α is given by a=rα.
mgsinθ−f=ma
where f is the frictional force.
τ=Iα=fr
fr=25mr2⋅ar
Simplifying gives:
f=25ma
mgsinθ−25ma=ma
Rearranging gives:
mgsinθ=ma+25ma=75ma
Thus, the acceleration a is:
a=5gsinθ7
The accelerations of the spheres are given by:
- For sphere 1: a1=5gsinθ17
- For sphere 2: a2=5gsinθ27
- For sphere 3: a3=5gsinθ37
sinθ1>sinθ2>sinθ3
Therefore:
a1>a2>a3
The sphere that rolls down the incline with the largest angle θ will have the greatest acceleration and will reach the bottom first. Thus, sphere 1 (with angle θ1) will reach the bottom first, followed by sphere 2, and then sphere 3.
Sphere 1 will reach the bottom first, followed by sphere 2, and then sphere 3.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - II
Explore 16 Videos
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:COMPREHENSION - III
Explore 1 Video
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
Explore 15 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Numerical Based Question Decimal Type
Explore 6 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
Similar Questions
Knowledge Check
If sinθ1+sinθ2+sinθ3=3 then cosθ1+cosθ2+cosθ3 is equal to
A3B2C1D0If the line −−→OR makes angles θ1,θ2,θ3 with the planes XOY,YOZ,ZOX respectively , then cos2θ1+cos2θ2+cos2θ3 is equal to
A1B2C3D4If sinθ1+sinθ2+sinθ3=3,thencosθ1+cosθ2+cosθ3=
A3B2C1D0
Three rods AB,BCand BD having thremal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in The ends A,C and D are at temperature θ1,θ2 and θ3 respectively Find the temperature of the junction B
(Assume steady state and θ1>θ>θ2>θ3)
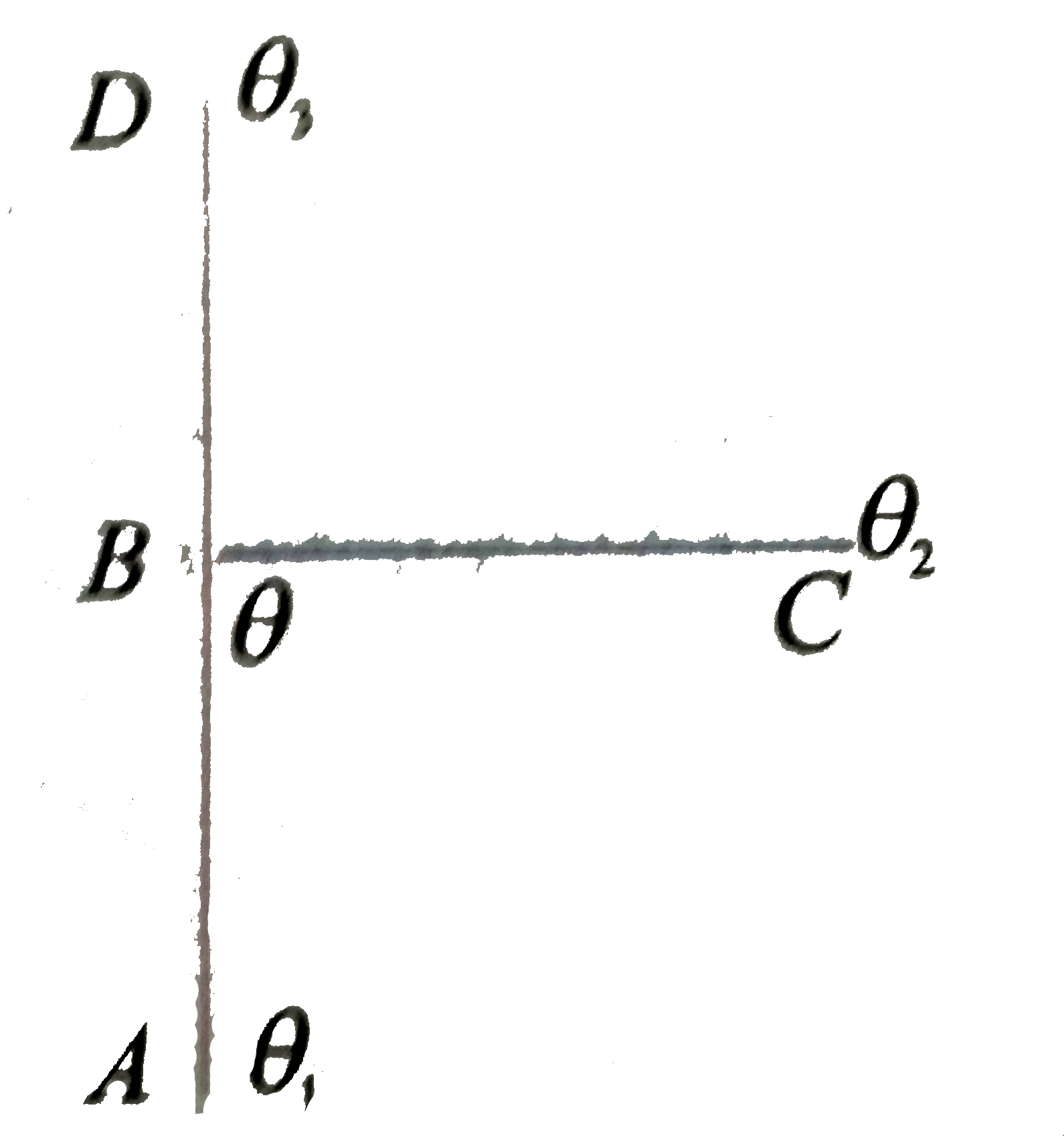 .
.
View SolutionThree ammeters — 1, 2 and 3 have different internal resistances r1,r2andr3 respectively. Internal resistance r1 is known but r2andr3 are unknown. The angular deflection of pointer in each ammeter is proportional to the current. Initially, the three ammeters were connected in series to a voltage source (fig. a) and deflections for the three ammeters were θ1,θ2andθ3 respectively. The three ammeters were then connected in parallel to the same voltage source (fig. b). This time the deflections were observed to be θ'1,θ'2 and θ'3 respectively.
(a) Find r2andr3.
(b) If θ2=θ3 but θ'3>θ'2 then which one is larger r2orr3 ?
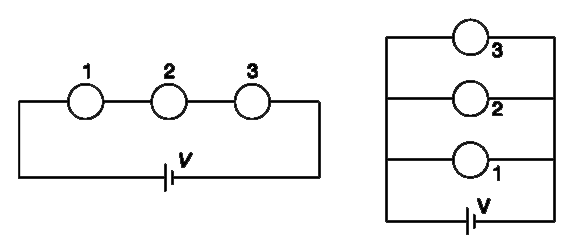
View SolutionLet L1,L2andL3 be the three normals to the parabola y2=4ax from point P inclined at the angle θ1,θ2andθ3 with x-axis, respectively. Then find the locus of point P given that θ1+θ2+θ3=α (constant).
View SolutionThe base of a triangle is divided into three equal parts. If θ1,θ2,θ3 be thw angles subtended by these parts at the vertex, then prove that
(cotθ1+cotθ2)(cotθ2+cotθ3)=4cosec2θ2
View SolutionIf the line passing through origin makes angles θ1,θ2,θ3 with the planes XOY, YOZ and ZOX, then sin2θ1+sin2θ2+sin2θ3=
View Solution