A ball of mass m = 1 kg rolling without slipping, strikes a smooth vertical wall and comes back. Before the impact the velocity of the ball is v1=10 cm/s and just after the impact v1=8 cm/s. Find the loss in energy of ball during the impact.
The correct Answer is:|ΔKE|=1.8×10−3J
To find the loss in energy of the ball during the impact, we will calculate the change in kinetic energy before and after the impact.
1. Identify the mass and velocities:
- Mass of the ball, m=1kg
- Initial velocity before impact, v1=10cm/s=0.1m/s (conversion from cm/s to m/s)
- Final velocity after impact, v2=8cm/s=0.08m/s (conversion from cm/s to m/s)
2. Calculate the initial kinetic energy (KE_initial):
KEinitial=12mv21
Plugging in the values:
KEinitial=12×1×(0.1)2=12×1×0.01=0.005J
3. Calculate the final kinetic energy (KE_final):
KEfinal=12mv22
Plugging in the values:
KEfinal=12×1×(0.08)2=12×1×0.0064=0.0032J
4. Calculate the loss in kinetic energy (ΔKE):
ΔKE=KEinitial−KEfinal
Plugging in the values:
ΔKE=0.005J−0.0032J=0.0018J
5. Conclusion:
The loss in energy of the ball during the impact is 0.0018J or 1.8×10−3J.
- Mass of the ball, m=1kg
- Initial velocity before impact, v1=10cm/s=0.1m/s (conversion from cm/s to m/s)
- Final velocity after impact, v2=8cm/s=0.08m/s (conversion from cm/s to m/s)
KEinitial=12mv21
Plugging in the values:
KEinitial=12×1×(0.1)2=12×1×0.01=0.005J
KEfinal=12mv22
Plugging in the values:
KEfinal=12×1×(0.08)2=12×1×0.0064=0.0032J
ΔKE=KEinitial−KEfinal
Plugging in the values:
ΔKE=0.005J−0.0032J=0.0018J
The loss in energy of the ball during the impact is 0.0018J or 1.8×10−3J.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - I
41 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - II
16 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I
15 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
A ball is falling a height of 50 m . It strikes the ground and rebounds to a height of 10 m . Calculate the velocity of the ball just before and after the collision . Also find the loss of kinectic energy of the ball during its collisio with ground .
View SolutionA ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
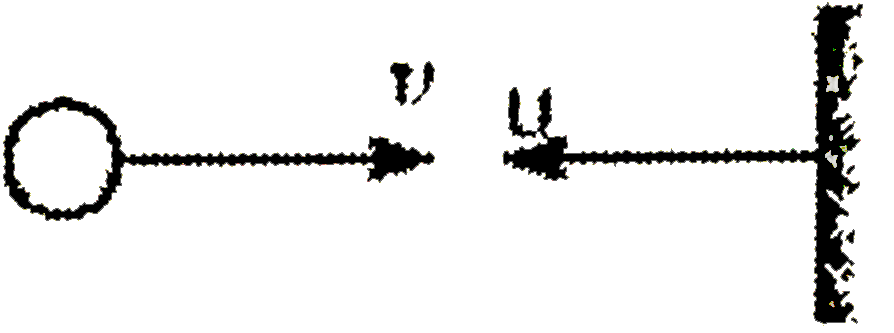
View Solution
Knowledge Check
A ball of mass 250 g moving with 20 m/s strikes a vertical wall and rebounds along the same line with a velocity of 15 m/s. If the time of contact is 0.1 s, the force exerted by the wall on the ball is
A87.5 NB12.5 NC−12.5 ND−87.5 NA ball of mass m1 moving with a certain speed collides elastically with another ball of mass m2 kept at rest . If the first ball starts moving in reversed direction after the impact then
Am1=m2Bm1>m2Cm1<m2DNone of theseA ball of mass 3 kg moving with a velocity of 3m/s collides with another ball of mass 1 kg moving with velocity u in the opposite direction. If the first ball comes to rest after the impact and e=2/7, then u is in m/s, is
A133B173C193D233
A thin uniform square plate with side l and mass M can rotate freely about a stationary vertical axis coinciding with one of its sides. A small ball of mass m flying with velocity v at right angles to the plate strikes elastically the centre of it. Find:
(a) the velocity of the ball v′ after the impact,
(b) the horizontal component of the resultant force which the axis will exert on the plate after the impact.
View SolutionA thin uniform square plate with side l and mass M can rotate freely abouta stationary vertical axis coinciding with one of its sides . A small ball of mass m flying with velocity v at right angles to the plate strikes elastically to the centre of it. Find the velocity of the ball v'after the impact and the horizontal component of the force which the axis will exert on the plate after the impact.
[3m−4M3m+4Mv,72Mm2v2l(3m+4m)2]
View SolutionA ball of mass 5 kg moving velocity 3m/s impinges direction on another ball of mass 2 kg moving with velocity 0.5m/s towards the first ball. Find the velocity after impact, if e=47
View SolutionA ball of mass 3 kg moving with a velocity of 3m/s collides with another ball of mass 1 kg moving with velocity u in the opposite direction. If the first ball comes to rest after the impact and e=2/7, then u is in m/s, is
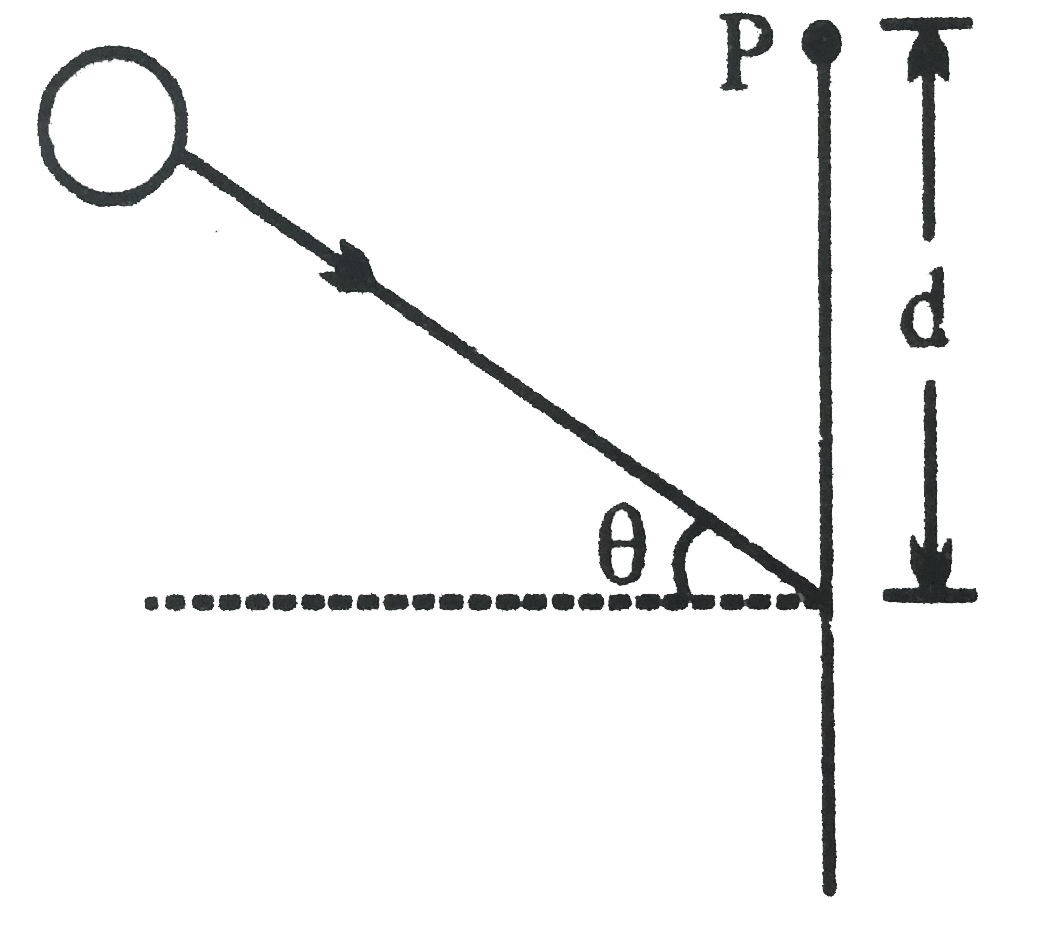
View SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
 .
.
View Solution
