A disc of radius R and mass m is mounted on a vertical axis through its centre and perendicular to its plane. A rat of same mass m runs around the rim of the disc with speed v anticlockwise relative to stationary observer. The disc rotates clockwise with angular speed omega. The rat finds a piece of bread on the rim and stops. Find the angular velocity of the disc after the rat stops.
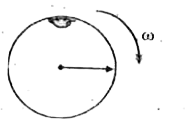
The correct Answer is:(ωR−2v)/3R
Step by step video, text & image solution for A disc of radius R and mass m is mounted on a vertical axis through its centre and perendicular to its plane. A rat of same mass m runs around the rim of the disc with speed v anticlockwise relative to stationary observer. The disc rotates clockwise with angular speed omega. The rat finds a piece of bread on the rim and stops. Find the angular velocity of the disc after the rat stops. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - I
41 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - II
16 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I
15 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :
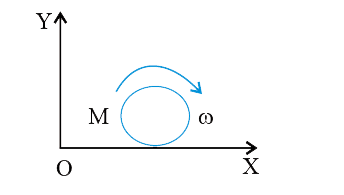
View Solution
Knowledge Check
A uniform disc of radius R and mass M can rotate on a smooth axis passing through its centre and perpendicular to its plane. A force F is applied on its rim. See fig. What is the tangential acceleration
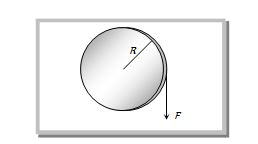 A2FMBFMCF2MDF4M
A2FMBFMCF2MDF4MA heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
AincreaseBdecreaseCbecomes zeroDremain unchangedA disc of mass 4 kg and radius 0.2 m, makes 20 rev/s, about an axis passing through its centre and perpendicular to the plane of the disc. The angular momentum of the disc is approximately equal to
A10 kg-m2/secB5 kg-m2/secC15 kg-m2/secD20 kg-m2/sec
A uniform disc of mass m and radius R I rotated about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficnet of friction between te disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View SolutionA disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
View SolutionA disc of radius 10 cm can rotate about an axis passing through its centre and perpendicular to its plane. A force of 10 N is applied along the tangent in the plane of the disc. If the moment of inertia of the disc about its centre is 5kgm2, then the increase in the angular velocity of the disc in 10 s will be
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
View Solution
