An objects is projected vertically upwards from the surface of the earth with a velocity 3 times the escape velocity ve from earth's surface. What will be its final velocity after escape from the earth's gravitational pull ?
√2ve
2√2ve
2ve
ve√2
The correct Answer is:B
To solve the problem, we need to determine the final velocity of an object that is projected vertically upwards from the surface of the Earth with a velocity three times the escape velocity.
Given:
- Escape velocity from the Earth's surface, ve=√2GMR
- Initial velocity of the object, v=3ve
Steps to Solve:
1. Calculate the Escape Velocity:
The escape velocity from the surface of the Earth is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
2. Initial Kinetic Energy:
The initial kinetic energy (KE) of the object when it is projected is:
KEi=12mv2=12m(3ve)2=12m(9v2e)=92mv2e
3. Initial Potential Energy:
The initial gravitational potential energy (PE) at the surface of the Earth is:
PEi=−GMmR
4. Total Mechanical Energy at the Surface:
The total mechanical energy (E) at the surface of the Earth is the sum of the initial kinetic energy and potential energy:
E=KEi+PEi=92mv2e−GMmR
5. Final Potential Energy at Infinity:
As the object escapes the gravitational pull of the Earth, its potential energy at infinity becomes zero:
PEf=0
6. Final Kinetic Energy at Infinity:
The total mechanical energy must remain constant. Therefore, at infinity:
E=KEf+PEf
E=KEf+0=KEf
Thus, we have:
KEf=92mv2e−GMmR
7. Setting Up the Equation:
We know that v2e=2GMR, so we can substitute this into our equation:
KEf=92mv2e−GMmR=92m(2GMR)−GMmR
KEf=9GMmR−GMmR=8GMmR
8. Final Velocity:
The final kinetic energy can also be expressed in terms of the final velocity vf:
KEf=12mv2f
Setting the two expressions for kinetic energy equal gives:
12mv2f=8GMmR
Dividing both sides by m and multiplying by 2:
v2f=16GMR
Taking the square root:
vf=√16GMR=4ve
Final Answer:
The final velocity of the object after escaping from the Earth's gravitational pull is 4ve.
- Escape velocity from the Earth's surface, ve=√2GMR
- Initial velocity of the object, v=3ve
The escape velocity from the surface of the Earth is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
The initial kinetic energy (KE) of the object when it is projected is:
KEi=12mv2=12m(3ve)2=12m(9v2e)=92mv2e
The initial gravitational potential energy (PE) at the surface of the Earth is:
PEi=−GMmR
The total mechanical energy (E) at the surface of the Earth is the sum of the initial kinetic energy and potential energy:
E=KEi+PEi=92mv2e−GMmR
As the object escapes the gravitational pull of the Earth, its potential energy at infinity becomes zero:
PEf=0
The total mechanical energy must remain constant. Therefore, at infinity:
E=KEf+PEf
E=KEf+0=KEf
Thus, we have:
KEf=92mv2e−GMmR
We know that v2e=2GMR, so we can substitute this into our equation:
KEf=92mv2e−GMmR=92m(2GMR)−GMmR
KEf=9GMmR−GMmR=8GMmR
The final kinetic energy can also be expressed in terms of the final velocity vf:
KEf=12mv2f
Setting the two expressions for kinetic energy equal gives:
12mv2f=8GMmR
Dividing both sides by m and multiplying by 2:
v2f=16GMR
Taking the square root:
vf=√16GMR=4ve
The final velocity of the object after escaping from the Earth's gravitational pull is 4ve.
Topper's Solved these Questions
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assigment problems (Objective) (level-I) Assertion & Reasoning type
2 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assigment problems (Objective) (level-II)
20 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assigment problems (Subjective) (level II & III)
15 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Video
Similar Questions
A body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionCompare the minimum velocity with which a particle must be projected vertically upwards from the surfaces of the earth in order that it may never return to the earth with that which is needed to make it escape from the earth ' s gravitational field .
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A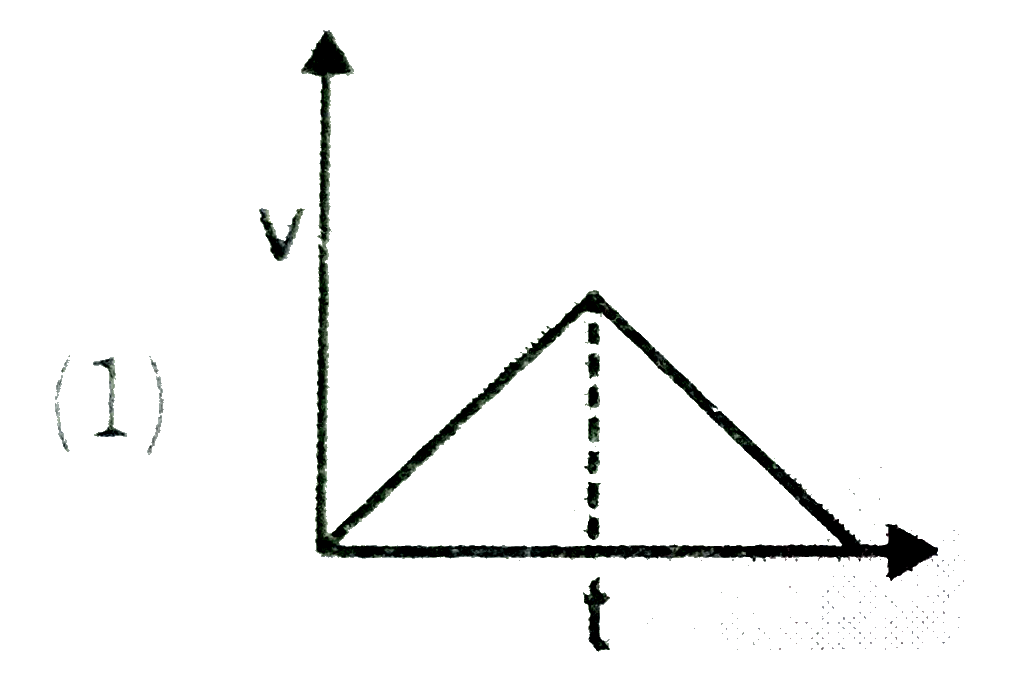 B
B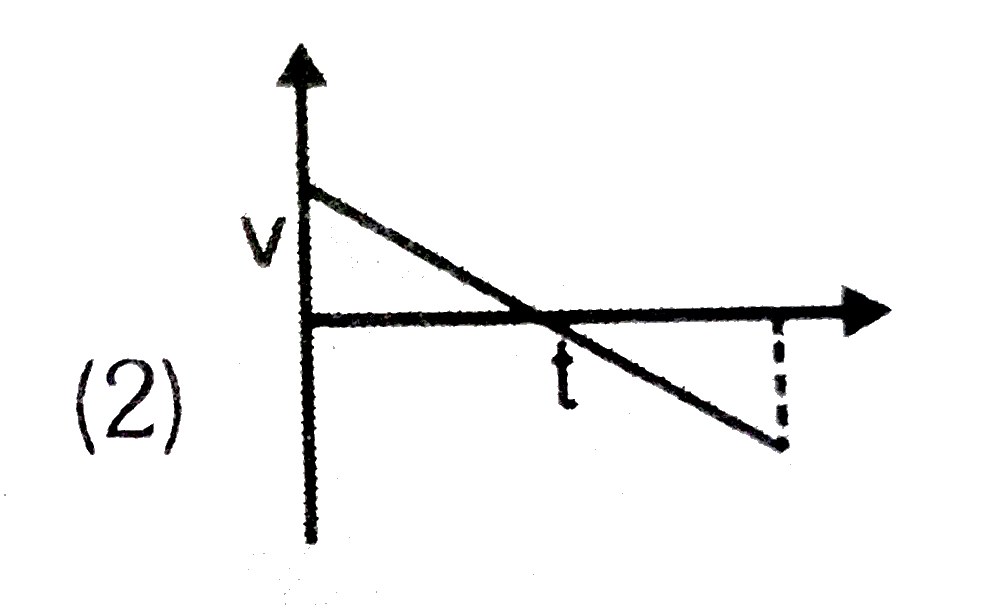 C
C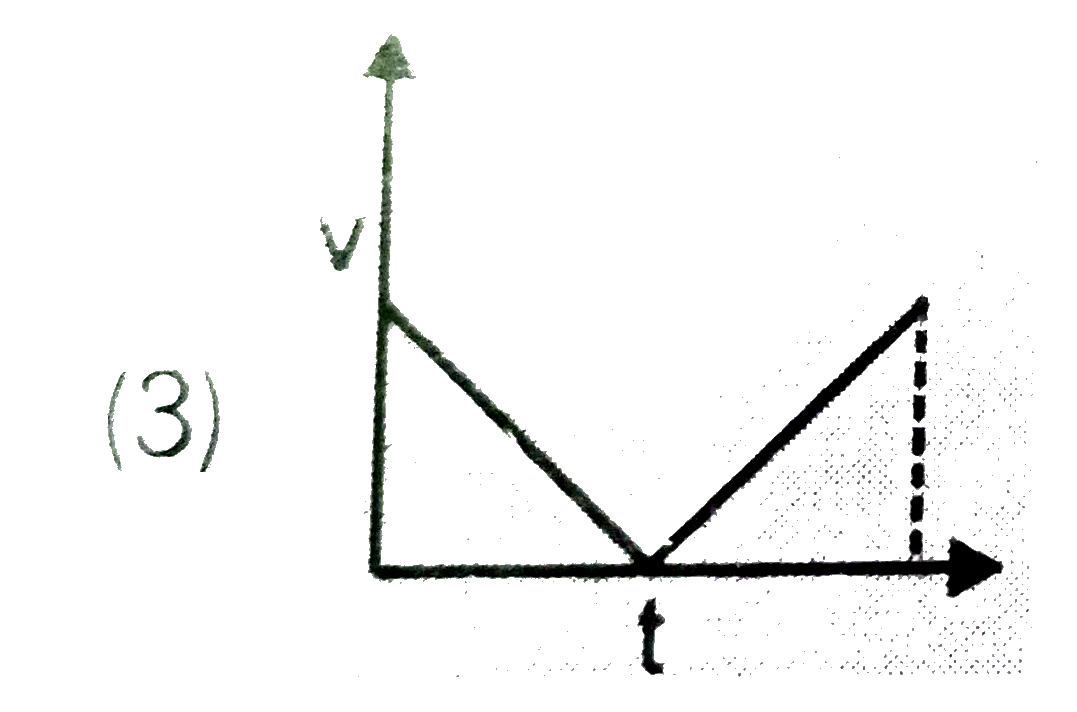 D
D
A body is projected from the surface of the earth with thrice the escape velocity (Ve) from the surface of the earth. What will be its velocity, when it will escape the gravitational pull?
A2√2VeB2VeCVe2D4VeThe escape velocity of a body from the surface of earth is
A11.2 km/sB11.4 km/sC11.6 km/sD11.0 km/s
A body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.
View SolutionA body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
View SolutionThe escape velocity from the surface of the Earth is
View SolutionA body is imparted a velocity v from the surface of the earth. If v0 is orbital velocity and ve be the escape velocity then for :
View SolutionThe escape velocity of a body from the surface of the earth is equal to
View Solution

