If the velocity of flow increases inside a tube , then at that point the pressure will _______.
To solve the question, we will use Bernoulli's equation, which relates the velocity of a fluid, its pressure, and its height at any point along a streamline.
1. Understanding Bernoulli's Equation:
Bernoulli's equation states that for an incompressible, frictionless fluid, the following relationship holds:
12ρV2+ρgh+P=constant
where:
- ρ = density of the fluid
- V = velocity of the fluid
- g = acceleration due to gravity
- h = height above a reference level
- P = pressure at that point
2. Identifying the Variables:
In the context of the question, we focus on a specific point in the tube where the velocity of flow increases. Let’s denote the pressure at that point as P, the velocity as V, and the height as h.
3. Analyzing the Situation:
- If the velocity V increases at that point, the term 12ρV2 will also increase.
- The height h remains constant as we are considering the same point in the tube.
4. Applying Bernoulli's Principle:
Since the sum of the three terms in Bernoulli's equation must remain constant, if 12ρV2 increases and ρgh remains constant, the pressure P must decrease to keep the equation balanced.
5. Conclusion:
Therefore, if the velocity of flow increases inside a tube, the pressure at that point will decrease.
Final Answer:
If the velocity of flow increases inside a tube, then at that point the pressure will decrease.
Bernoulli's equation states that for an incompressible, frictionless fluid, the following relationship holds:
12ρV2+ρgh+P=constant
where:
- ρ = density of the fluid
- V = velocity of the fluid
- g = acceleration due to gravity
- h = height above a reference level
- P = pressure at that point
In the context of the question, we focus on a specific point in the tube where the velocity of flow increases. Let’s denote the pressure at that point as P, the velocity as V, and the height as h.
- If the velocity V increases at that point, the term 12ρV2 will also increase.
- The height h remains constant as we are considering the same point in the tube.
Since the sum of the three terms in Bernoulli's equation must remain constant, if 12ρV2 increases and ρgh remains constant, the pressure P must decrease to keep the equation balanced.
Therefore, if the velocity of flow increases inside a tube, the pressure at that point will decrease.
If the velocity of flow increases inside a tube, then at that point the pressure will decrease.
Topper's Solved these Questions
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT PROBLEMS (SUBJECTIVE ) TRUE OR FALSE QUESTIONS (LEVEL-I)
Explore 6 Videos
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
Explore 15 Videos
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT PROBLEMS (SUBJECTIVE ) SHORT ANSWER TYPE QUESTIONS (LEVEL -I)
Explore 4 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
Similar Questions
It water flows horizontally through a pipe of varying cross section and the pressure of water equals 10cm of g at a point where the velocity of flow is 40cm/s, what is the pressure at another point where the velocity of flow is 50cm/s?
View SolutionWater is flowing through a horizontal pipe of varying cross-section. If the pressure of water equals 2 cm of Hg where velocity of flow is 32cms−1, what is the pressure at another point where the velocity of flow is 40cms−1?
View Solution
Knowledge Check
Water flows steadily through a horizontal pipe of a variable cross-section. If the pressure of water is p at a point where the velocity of flow is v, what is the pressure at another point where the velocity of flow is 2v, ρ being the density of water?
Ap+2ρv2Bp−2ρv2Cp+32ρv2Dp−32ρv2Water is flowing streamline motion through a horizontal tube. The pressure at a point in a tube is P where the velocity of flow is v. At another point where the pressure isp2, the velocity of flow is (density of water = ρ)
A√v2+pρB√v2−pρC√v2+2pρD√v2−2pρAn idel fluid is flowing in a tube of varying corss- section .At some point the radius of the tube is r and the velocity of flow is v .The velocity of flow at another point, where the radius is r/2 is :
Av/4Bv/2C2vD4v
Increase in pressure____ the melting point of ice.
View SolutionWith the increase in pressure, the boiling point of the liquid ______
View SolutionWater is flowing in streamline motion in the tube shown in fig. pressure is
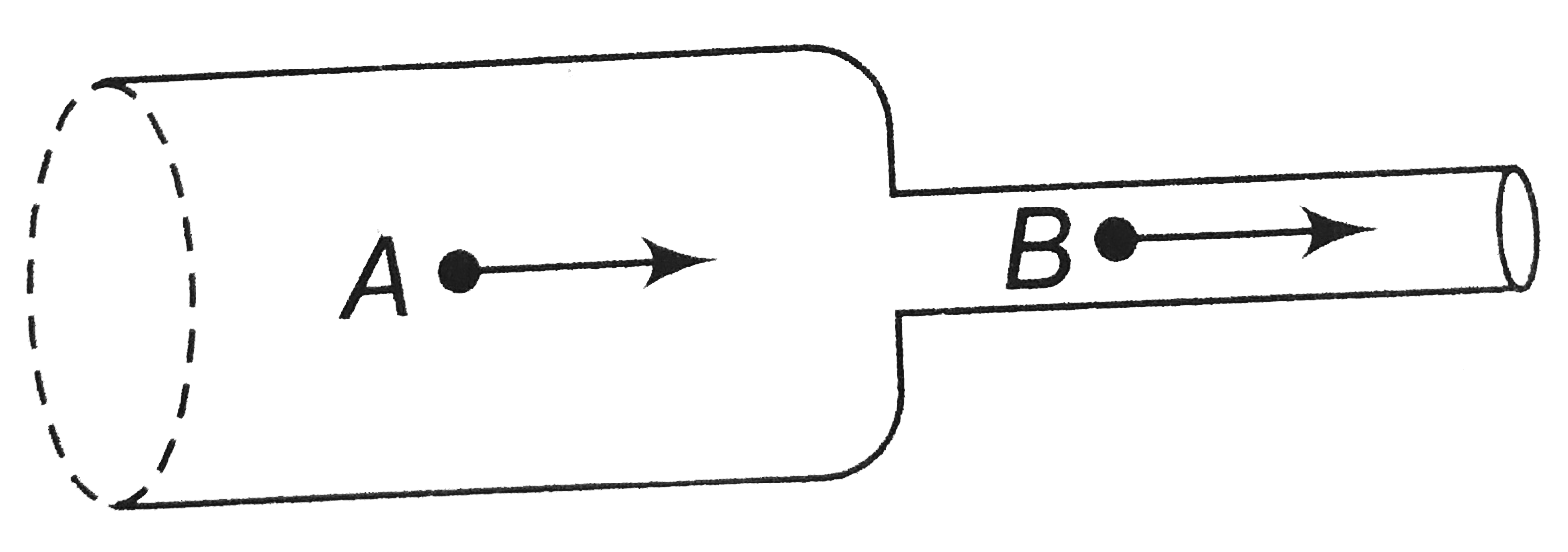
View SolutionWater flows steadily through a horizontal pipe of variable cross-section. If the pressure of water is p at a point where the velocity of flow is v, at another point (pressure p'), where the velocity of flow in ηv : The following statements are given below
View SolutionWith the increase in pressure, the boiling point of the liquid ______
View Solution