A weightless rigid rod AB of length / connects two equal masses m one particle is fixed at the end B and the other at the middle ofthe rod as shown in the figure-5.131. The rod can rotate in the vertical plane freely around the hinge point/4. Choose the correct option(s)
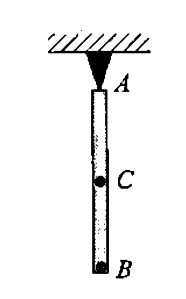
The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24gl5
The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24glg
The ratio of compressive force in the rods AC and BC is 2:1 when the masses are at highest point.
The ratio of compressive force in the rods AC and BC is 3:1 when the masses are at highest point.
The correct Answer is:A, C
Step by step video, text & image solution for A weightless rigid rod AB of length / connects two equal masses m one particle is fixed at the end B and the other at the middle ofthe rod as shown in the figure-5.131. The rod can rotate in the vertical plane freely around the hinge point/4. Choose the correct option(s) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I) (ASSERTION REASONING TYPE)
2 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
A weightless rod of length 2l carries two equal masses 'm' , one secured at lower end A and the other at the middle of the rod at B. The rod can rotate in vertical plane about a fixed horizontal axis passing through C. What horizontal velocity must be imparted to the mass at A so that it just completes the vertical circle.
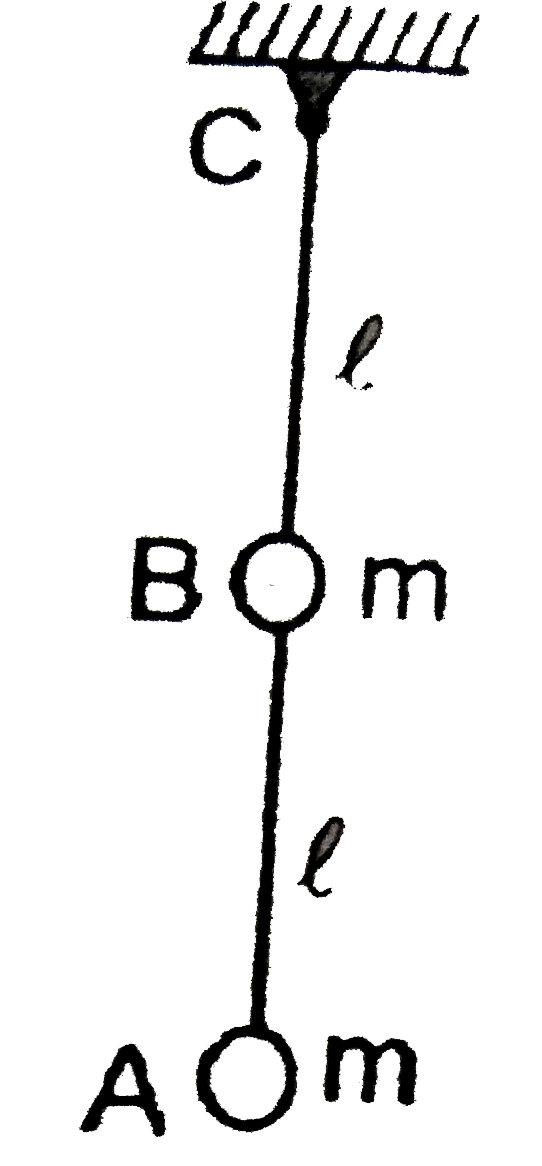
View SolutionA rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

View Solution
Knowledge Check
A weightless rod of length 2l carries two equal masses 'm', one tied at lower end A and the other at the middle of the rod at B. The rod can rotate in vertical plane about a fixed horizontal axis passing thriugh C . The rod of is released from rest in horizontal possion. The speed of the mass B at the instant rod become vertical is:
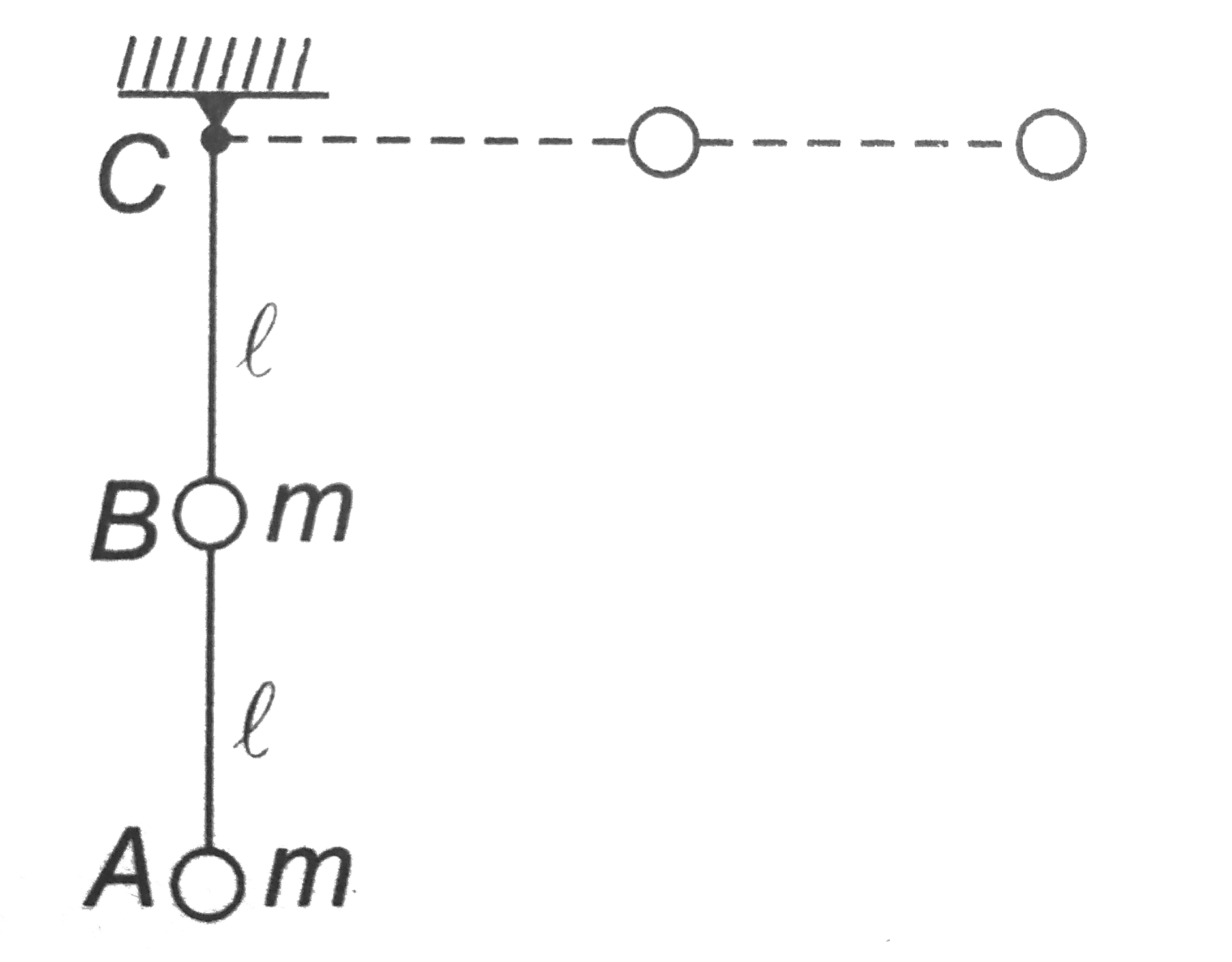 A√3gl5B√4gl5C√6gl5D√7gl5
A√3gl5B√4gl5C√6gl5D√7gl5A weightless rod of length l carries two equal masses m one fixed at the end and other in the middle ofhte rod. The rod can revolve in a vertical plane about A. Then, horizontal velocity which must be imparted to end C of rod to deflect it to horizontal position is
 A√125glB√3glC√165glD√2gl
A√125glB√3glC√165glD√2glA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?A47B57mgC137mgD117mg
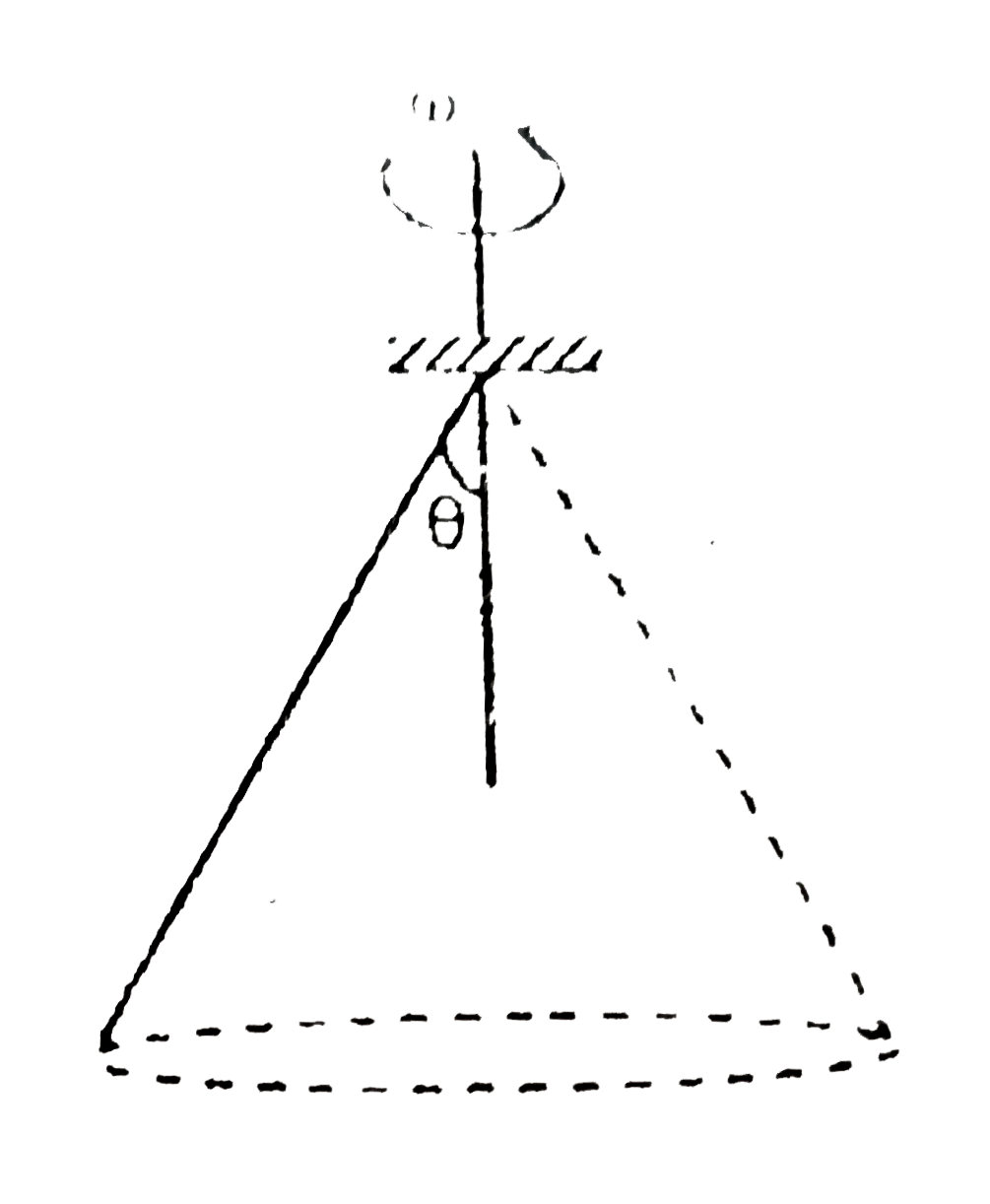
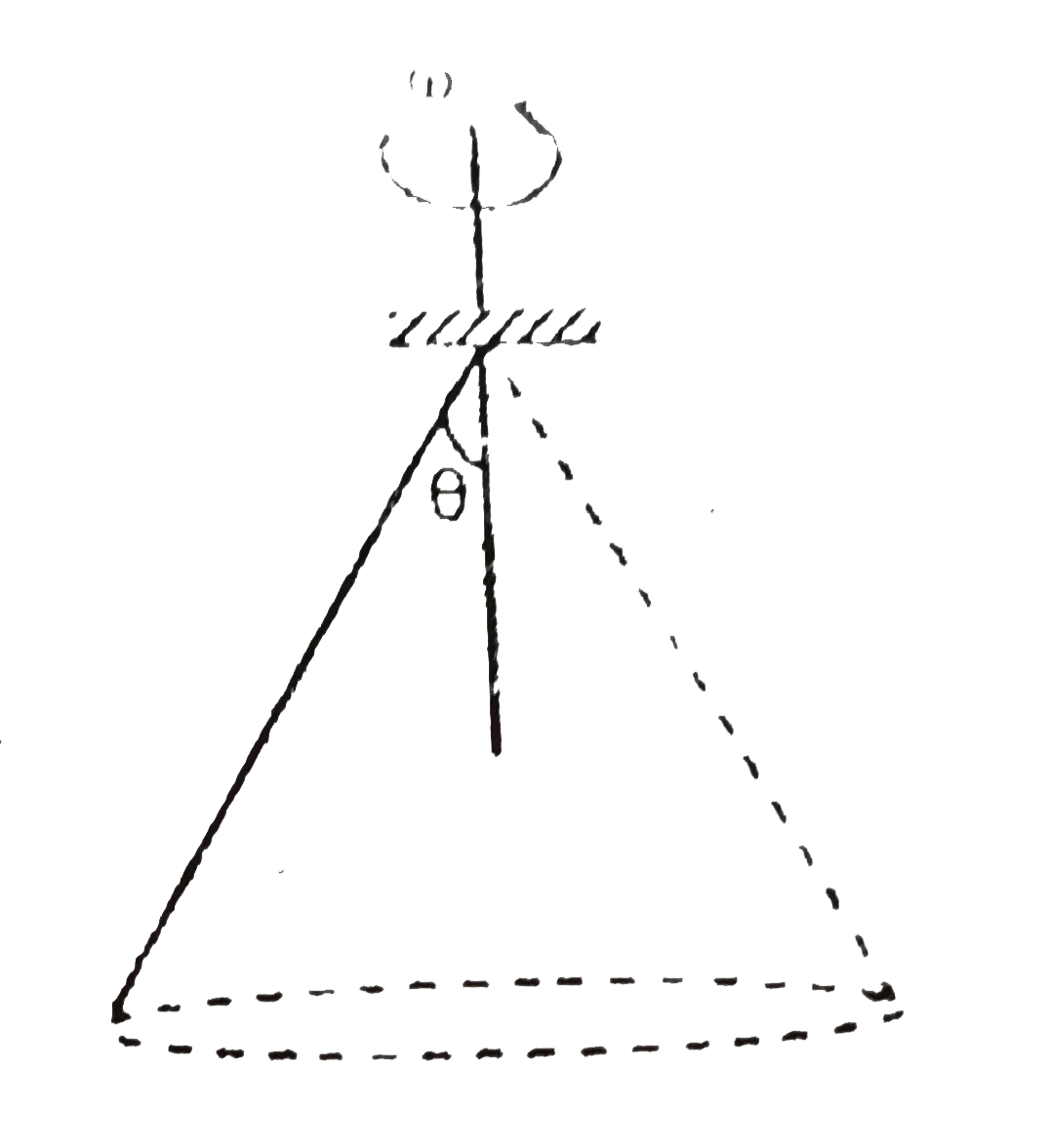
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
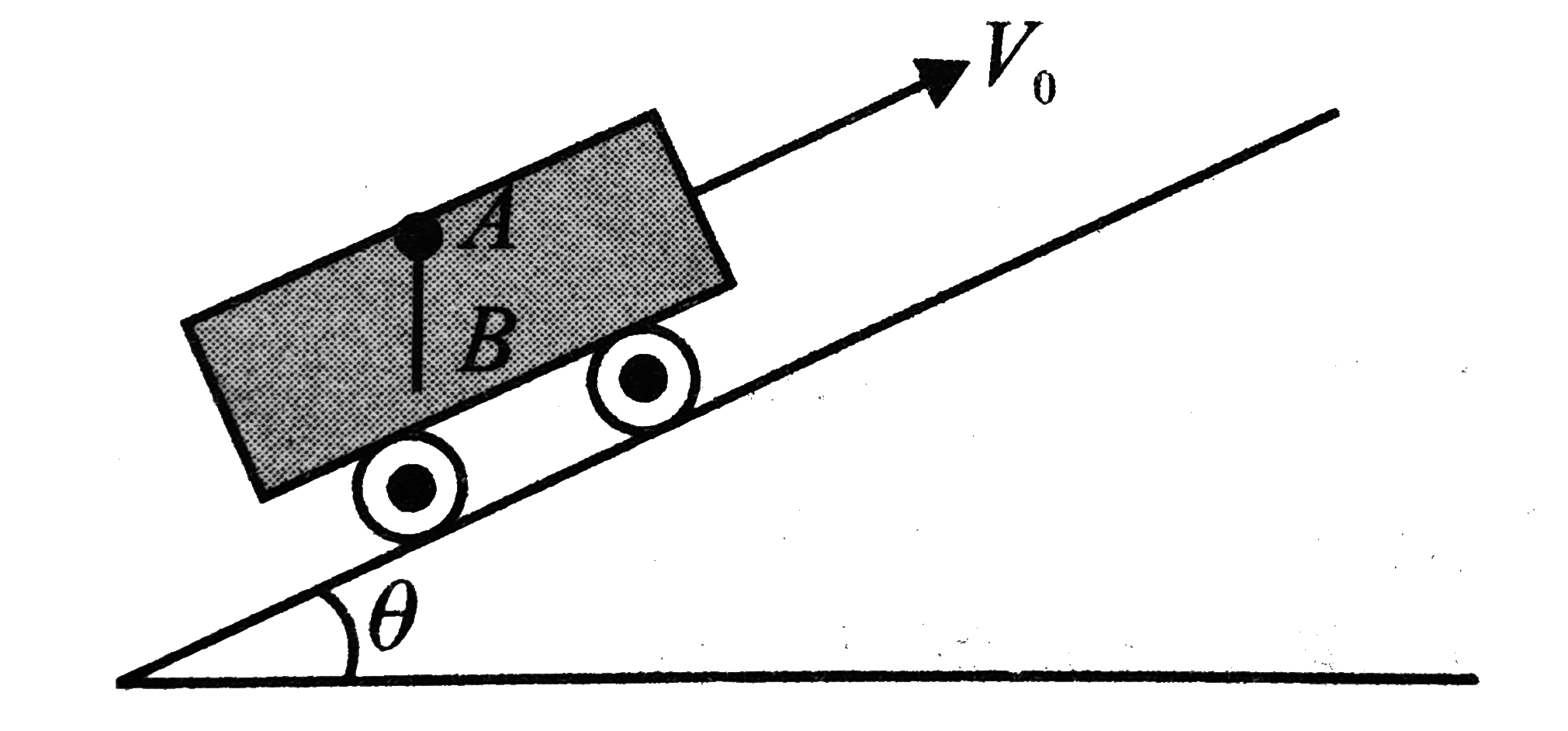
View SolutionA uniform rod AB of length l and mass m hangs from point A in a car moving with velocity v0 on an inclined plane as shown in Fig. The rod can rotate in vertical plane about the axis at point A. if the car suddenly stops, the angular speed with which the rod starts rotating is
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
