A block of mass 10 kg slides down on an incline 5 m long and 3 m high. A man pushes up on the ice block parallel to the incline so that it slides down at constant speed. The coefficient of friction between the ice and the incline is 0.1. Find :
(a) the work done by the man on the block.
(b) the work done by gravity on the block.
(c) the work done by the surface on the block.
(d) the work done by the resultant forces on the block.
(e) the change in K.E. of the block.
The correct Answer is:(a) −260 J
(b) =300 J
(c) −40 J
(d) zero
(e) zero
To solve the problem step by step, we will analyze the forces acting on the block and calculate the required work done by different forces.
Given Data:
- Mass of the block, m=10kg
- Length of incline, L=5m
- Height of incline, h=3m
- Coefficient of friction, μ=0.1
- Gravitational acceleration, g=10m/s2
Step 1: Calculate the angle of the incline
Using the right triangle formed by the height and length of the incline:
sinθ=hL=35andcosθ=45
Step 2: Calculate the gravitational force components
The gravitational force acting on the block is:
Fg=mg=10×10=100N
The components of the gravitational force along the incline:
Fg∥=mgsinθ=100×35=60N
F_{g \perpendicular} = mg \cos \theta = 100 \times \frac{4}{5} = 80 \, \text{N}
Step 3: Calculate the normal force
The normal force N is equal to the perpendicular component of the gravitational force:
N = F_{g \perpendicular} = 80 \, \text{N}
Step 4: Calculate the frictional force
The frictional force Ff opposing the motion is given by:
Ff=μN=0.1×80=8N
Step 5: Calculate the force exerted by the man
Since the block is sliding down at constant speed, the net force along the incline must be zero:
P+Ff=Fg∥
Thus, the force exerted by the man P is:
P=Fg∥−Ff=60−8=52N
Step 6: Calculate the work done by the man
The work done by the man Wm is:
Wm=P⋅d⋅cos(180∘)=52⋅5⋅(−1)=−260J
Step 7: Calculate the work done by gravity
The work done by gravity Wg is:
Wg=Fg∥⋅d=60⋅5=300J
Step 8: Calculate the work done by the surface (friction)
The work done by friction Wf is:
Wf=Ff⋅d⋅cos(180∘)=8⋅5⋅(−1)=−40J
Step 9: Calculate the work done by the resultant forces
Since the block moves with constant velocity, the net work done by the resultant forces Wr is:
Wr=0J
Step 10: Calculate the change in kinetic energy
Since the velocity is constant, the change in kinetic energy ΔKE is:
ΔKE=0J
Summary of Results:
(a) Work done by the man on the block: −260J
(b) Work done by gravity on the block: 300J
(c) Work done by the surface on the block: −40J
(d) Work done by the resultant forces on the block: 0J
(e) Change in K.E. of the block: 0J
- Mass of the block, m=10kg
- Length of incline, L=5m
- Height of incline, h=3m
- Coefficient of friction, μ=0.1
- Gravitational acceleration, g=10m/s2
Using the right triangle formed by the height and length of the incline:
sinθ=hL=35andcosθ=45
The gravitational force acting on the block is:
Fg=mg=10×10=100N
The components of the gravitational force along the incline:
Fg∥=mgsinθ=100×35=60N
F_{g \perpendicular} = mg \cos \theta = 100 \times \frac{4}{5} = 80 \, \text{N}
The normal force N is equal to the perpendicular component of the gravitational force:
N = F_{g \perpendicular} = 80 \, \text{N}
The frictional force Ff opposing the motion is given by:
Ff=μN=0.1×80=8N
Since the block is sliding down at constant speed, the net force along the incline must be zero:
P+Ff=Fg∥
Thus, the force exerted by the man P is:
P=Fg∥−Ff=60−8=52N
The work done by the man Wm is:
Wm=P⋅d⋅cos(180∘)=52⋅5⋅(−1)=−260J
The work done by gravity Wg is:
Wg=Fg∥⋅d=60⋅5=300J
The work done by friction Wf is:
Wf=Ff⋅d⋅cos(180∘)=8⋅5⋅(−1)=−40J
Since the block moves with constant velocity, the net work done by the resultant forces Wr is:
Wr=0J
Since the velocity is constant, the change in kinetic energy ΔKE is:
ΔKE=0J
(a) Work done by the man on the block: −260J
(b) Work done by gravity on the block: 300J
(c) Work done by the surface on the block: −40J
(d) Work done by the resultant forces on the block: 0J
(e) Change in K.E. of the block: 0J
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-II & III)
Explore 15 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I)
Explore 36 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) True or False Type Questions
Explore 3 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
A block of mass 5.0 kg slides down an incline of inclination 300 and length 10 m. The work done by the force of gravity (in joule) is
View SolutionA piece of ics slides down a 45∘ incline in twice the time it takes to slide down a frictionless 45∘ incline . What is the coefficient of friction between the ice and the incline ? .
View Solution
Knowledge Check
A block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
AsinθBcosθCcotθDtanθA block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
Asin θBcos θCgDtan θBlock A of mass M in the system shown in the figure slides down the incline at a constant speed. The coefficient of friction between block A and the surface is 1 3 3 . The mass of block B is-
 Am/2Bm/3C2m/3Dm/√3
Am/2Bm/3C2m/3Dm/√3
A block of mass 250 g slides down an incline of inclination 370 with a uniform speed. Find the work done against the friction as the block slides through 1.0 m.
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View SolutionA block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30∘ by a force of 10 N parallel to the inclined surface as shown in the figure.
The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, then the work against gravity is (Take g=10ms−2)
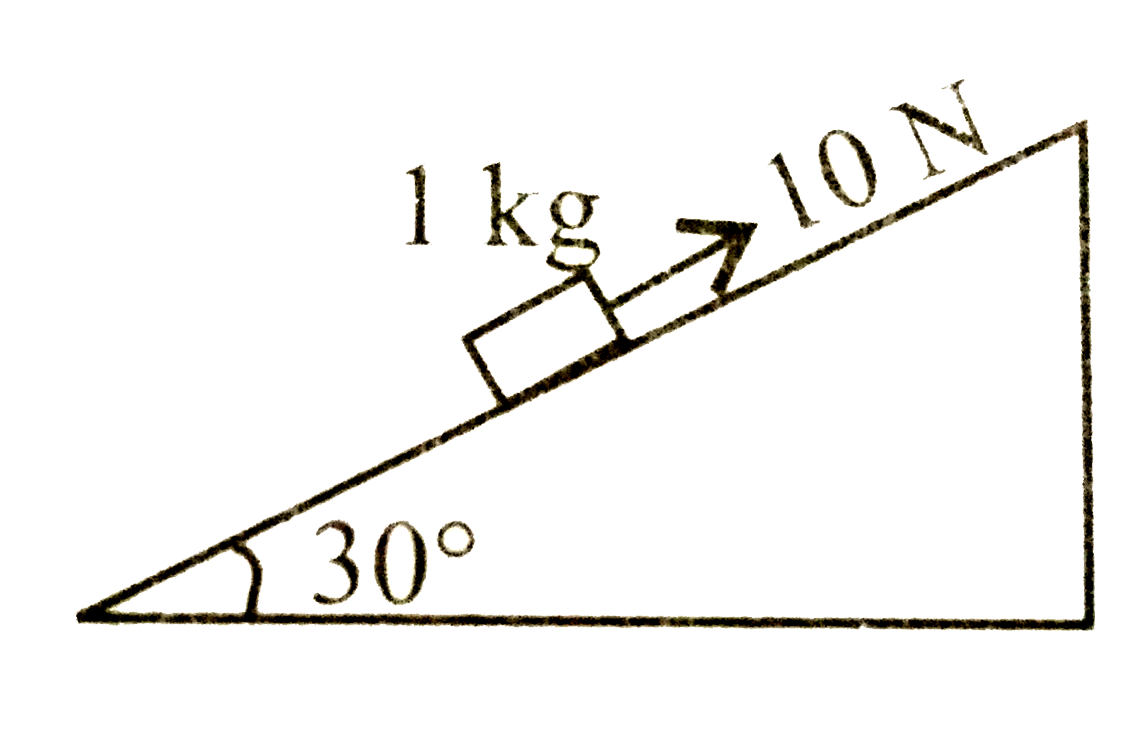
View SolutionA block of mas m begins to slide down on an inclined plane of inclination θ. The force of friction will be
View Solution