A particle is moving in such a way that at one instant velocity vector of the particle is 3ˆi+4ˆjm/s and acceleration vector is −25ˆi−25ˆjm/s? The radius of curvature of the trajectory of the particle at that instant is
2 m
3 m
5 m
10 m
The correct Answer is:C
To find the radius of curvature of the trajectory of the particle given its velocity and acceleration vectors, we can follow these steps:
1. Identify the Given Vectors:
- Velocity vector v=3^i+4^j m/s
- Acceleration vector a=−25^i−25^j m/s²
2. Calculate the Magnitude of Velocity:
|v|=√(3)2+(4)2=√9+16=√25=5 m/s
3. Determine the Angle of the Velocity Vector:
- The angle θ with respect to the horizontal can be calculated using:
tan(θ)=43
- Therefore, θ=tan−1(43).
4. Find the Components of Acceleration:
- The acceleration vector can be broken down into components:
- ax=−25 m/s²
- ay=−25 m/s²
5. Calculate the Perpendicular Component of Acceleration:
- The angle of the velocity vector is 53∘ (from the previous calculation).
- The angle of the acceleration vector is 53∘+90∘=143∘.
- The perpendicular component of the acceleration can be calculated using:
a_{\perpendicular} = |\mathbf{a}| \cdot \sin(37^\circ)
- Where 37∘ is the complementary angle to 53∘:
|a|=√(−25)2+(−25)2=√625+625=√1250=25√2 m/s2
- The sine of 37∘ is 35:
a_{\perpendicular} = 25 \cdot \frac{3}{5} = 15 \text{ m/s}^2
6. Calculate the Radius of Curvature:
- The radius of curvature R can be calculated using the formula:
R = \frac{v^2}{a_{\perpendicular}}
- Substituting the values:
R=(5)215=2515=53 m
Final Answer:
The radius of curvature of the trajectory of the particle at that instant is 53 m.
- Velocity vector v=3^i+4^j m/s
- Acceleration vector a=−25^i−25^j m/s²
|v|=√(3)2+(4)2=√9+16=√25=5 m/s
- The angle θ with respect to the horizontal can be calculated using:
tan(θ)=43
- Therefore, θ=tan−1(43).
- The acceleration vector can be broken down into components:
- ax=−25 m/s²
- ay=−25 m/s²
- The angle of the velocity vector is 53∘ (from the previous calculation).
- The angle of the acceleration vector is 53∘+90∘=143∘.
- The perpendicular component of the acceleration can be calculated using:
a_{\perpendicular} = |\mathbf{a}| \cdot \sin(37^\circ)
- Where 37∘ is the complementary angle to 53∘:
|a|=√(−25)2+(−25)2=√625+625=√1250=25√2 m/s2
- The sine of 37∘ is 35:
a_{\perpendicular} = 25 \cdot \frac{3}{5} = 15 \text{ m/s}^2
- The radius of curvature R can be calculated using the formula:
R = \frac{v^2}{a_{\perpendicular}}
- Substituting the values:
R=(5)215=2515=53 m
The radius of curvature of the trajectory of the particle at that instant is 53 m.
Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I (ASSERTION REASONING TYPE)
Explore 2 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II
Explore 20 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-II & III
Explore 15 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
A particle is moving in an isolated x−y plane. At an instant, the particle has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2. At that instant what will be the radius of curvature of its path ?
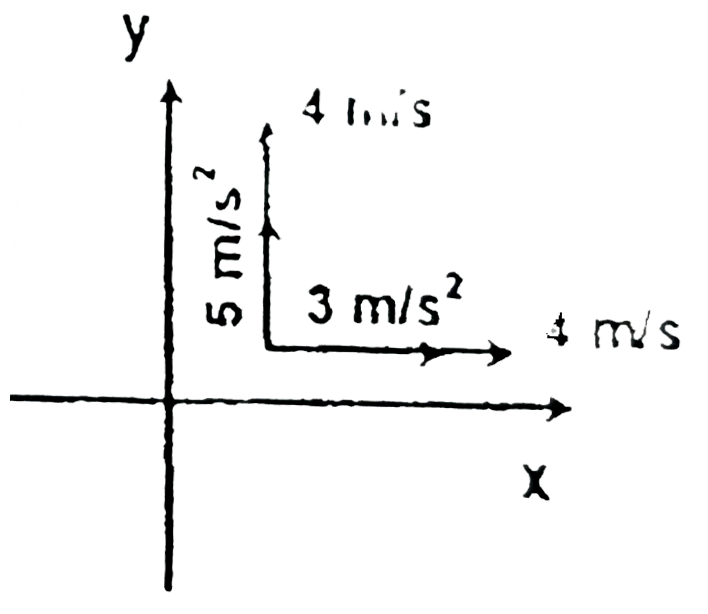
View SolutionA particle is moving in x-y plane. Its initial velocity and acceleration are u=(4ˆi+8ˆj)m/sanda=(2ˆi−4ˆj)m/s2. Find
(a) the time when the particle will cross the x-axis.
(b) x-coordinate of particle at this instant.
(c) velocity of the particle at this instant.
Initial coordinates of particle are (4m,10m).
View Solution
Knowledge Check
A particle moves in plane with acceleration →a=2ˆi+2ˆj. If →v=3ˆi+6ˆj, then final velocity of particle at time t=2s is
A5ˆi+8ˆjB7ˆi+10ˆjC2ˆi+6ˆjD3ˆi+2ˆjA particle has an initial velocity of 3ˆi+4ˆj and on acceleration of 0.4ˆj+0.3ˆj . The magnitude of its velocity after 10 s is
A7√2 unitsB7 unitsC8.5 unitsD10 units .A particle is moving with a constant acceleration →a=ˆi−2ˆj+2ˆkm/s2 and instantaneous velocity →v=ˆi+2ˆj+2ˆkm/s, then rate of change of speed of particle 2 second after this instant will be :
A193m/s2B3m/s2C197m/s2DNone of these
The velocity of a particle at t=0is→U=4ˆi+3ˆjm/sec and a constant acceleration is →a=6ˆi+4ˆjm/sec2. Find the velocity and displacement of the particle at t=2sec.
View SolutionA particle is given an initial velocity of →u=(3ˆi+4ˆj)m/s. Acceleration of the particle is →a=(3t2+2tˆj)m/s2. Find the velocity of particle at t=2s.
View SolutionA particle has an initial velocity 3ˆi+4ˆj and an accleration of 0.4ˆi+0.3ˆj. Its speed after 10s is
View SolutionA particle leaves the origin with an initial velocity →v=3ˆi m/s and a constant acceleration →a=(−ˆi−0.5ˆj)m/s2 in free space. Its velocity →v and position vector →r when it reaches its maximum x-coordinate are
View SolutionA particle has an initial velocity of 4ˆi+3ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is
View Solution

