A ball with mass m projected horizontally off the end of a table with an initial kinectic energy k. At a time t after it leaves the end of the table it has kinectic energy 3k.The time t is n/gsqrt(k/m).Find the value of n Neglect air resistance.
The correct Answer is:2
To solve the problem, we need to analyze the motion of the ball after it is projected horizontally off the table.
1. Understanding Initial Conditions:
- The ball is projected horizontally with an initial kinetic energy k.
- The initial kinetic energy can be expressed as:
k=12mv2x
where m is the mass of the ball and vx is the horizontal component of the velocity.
2. Kinetic Energy After Time t:
- At time t, the kinetic energy of the ball is given as 3k.
- The total kinetic energy at this time can be expressed as:
3k=12m(v2x+v2y)
where vy is the vertical component of the velocity after time t.
3. Relating the Two Kinetic Energies:
- From the initial kinetic energy:
k=12mv2x⟹v2x=2km
- Substituting this into the equation for 3k:
3k=12m(2km+v2y)
- Simplifying this gives:
3k=k+12mv2y
- Rearranging yields:
2k=12mv2y⟹v2y=4km
4. Finding the Vertical Velocity:
- The vertical velocity vy can be expressed as:
vy=√4km=2√km
5. Using Kinematics to Relate Time and Velocity:
- The vertical motion of the ball is influenced by gravity. The vertical velocity vy after time t can also be expressed using the equation of motion:
vy=gt
- Equating the two expressions for vy:
gt=2√km
6. Solving for Time t:
- Rearranging gives:
t=2√kmg
7. Expressing Time in Given Form:
- The problem states that t=ng√km.
- Setting the two expressions for t equal to each other:
2√kmg=ng√km
- Cross-multiplying gives:
2(√km)2=n
- Since (√km)2=km:
n=2⋅km
8. Finding the Value of n:
- From the previous steps, we find n=2.
Final Answer:
The value of n is 2.
- The ball is projected horizontally with an initial kinetic energy k.
- The initial kinetic energy can be expressed as:
k=12mv2x
where m is the mass of the ball and vx is the horizontal component of the velocity.
- At time t, the kinetic energy of the ball is given as 3k.
- The total kinetic energy at this time can be expressed as:
3k=12m(v2x+v2y)
where vy is the vertical component of the velocity after time t.
- From the initial kinetic energy:
k=12mv2x⟹v2x=2km
- Substituting this into the equation for 3k:
3k=12m(2km+v2y)
- Simplifying this gives:
3k=k+12mv2y
- Rearranging yields:
2k=12mv2y⟹v2y=4km
- The vertical velocity vy can be expressed as:
vy=√4km=2√km
- The vertical motion of the ball is influenced by gravity. The vertical velocity vy after time t can also be expressed using the equation of motion:
vy=gt
- Equating the two expressions for vy:
gt=2√km
- Rearranging gives:
t=2√kmg
- The problem states that t=ng√km.
- Setting the two expressions for t equal to each other:
2√kmg=ng√km
- Cross-multiplying gives:
2(√km)2=n
- Since (√km)2=km:
n=2⋅km
- From the previous steps, we find n=2.
The value of n is 2.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Matrix match type
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Comprehension
4 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Assertion reason type
1 Video
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Video
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A ball is projected in a manner such that its horizontal gange is n times of the maximum height. Then find out the ratio of potential energy to kinetic energy at maximum height.
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View Solution
Knowledge Check
In S.H.M., the graph between kinetic energy K and time 't' is
A B
B C
C D
D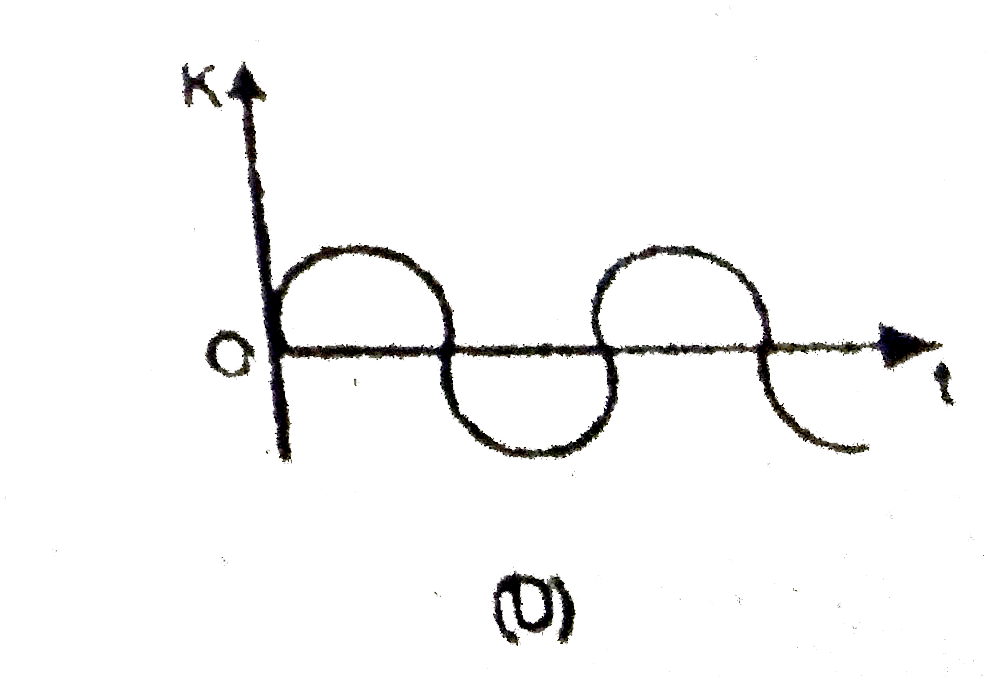
A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
AFt2mBF2t22mCFt22mDF2t23mA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
Ap2t2mBp2t22mCp2t23mDpt2m
Two particle A and B, of mass 3mand2m respectively, are attached to the ends of a light inextensible string which passes over a smooth fixed pulley of negligible mass. After the system is released and A falls through a distance L, it hits a horizontal inelastic table so that its speed is immediately reduced to zero. Assume that B never hits the table or the pulley. Find
(a) the time for which A is resting on the table after the first collision and before it is jerked off,
(b) the difference between the total kinetic energy of the system immediately before A first hits the table and total kinetic energy immediately after A starts moving upwards for the first time. Explain the loss in kinetic energy.

View SolutionA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View Solution
