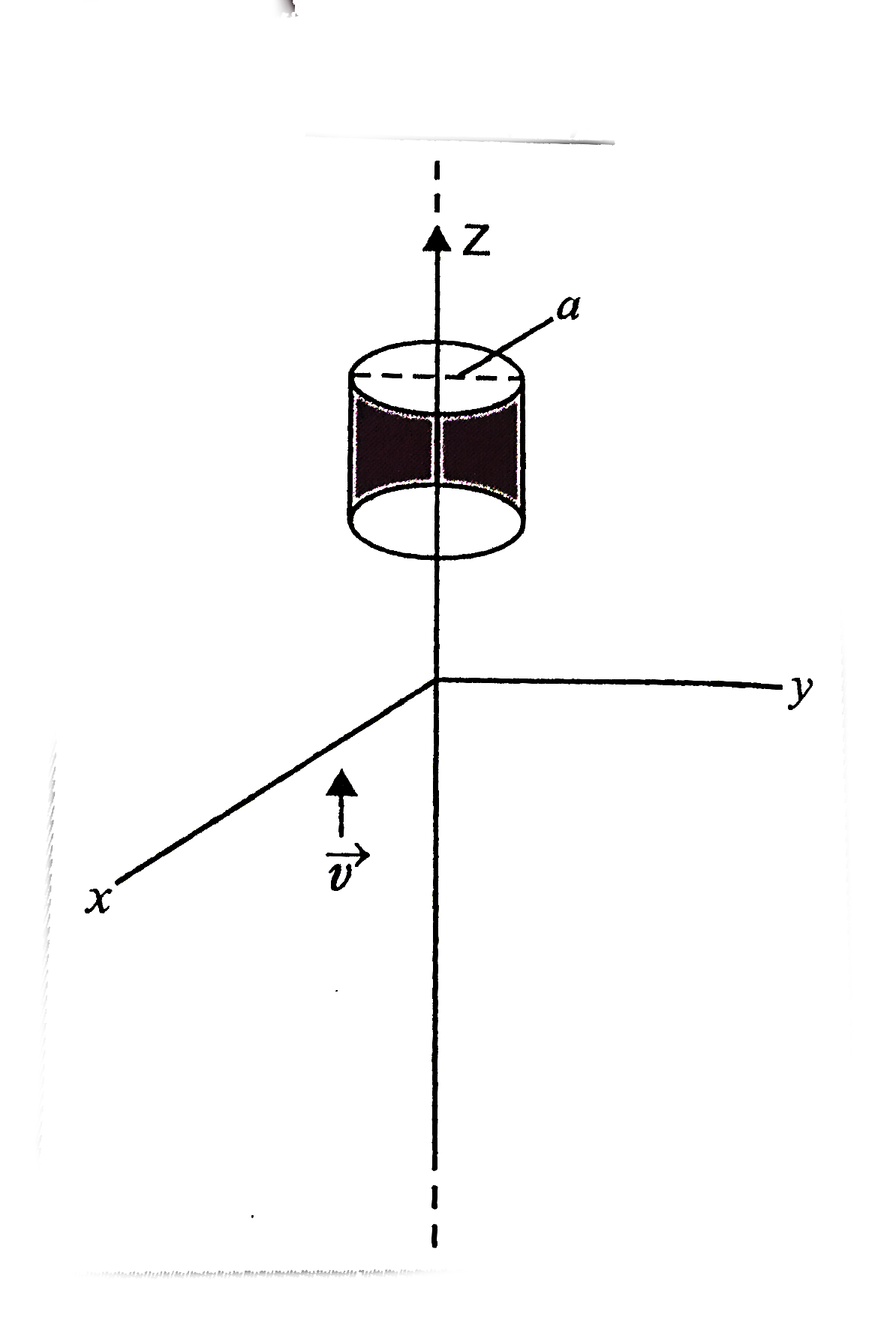
An infinitely long thin wire carrying a uniform linear static charge density λ is placed along the z-axis Fig. The wire is set into motion along its length with a uniform velocity →v=vˆk. Calculate the poynting vector →S=1μ0(→E×→B).
−λ2v4π2ε0a2ˆk
λ2v4π2ε0a2ˆi
λ2v4π2ε0a2ˆk
−λ2v4π2ε0a2ˆi
The correct Answer is:A
We know that
→B=μ0I2πaˆi=μ02πλvaˆi,→E=λˆj2πε0a
→S=1μ0[→E×→B]
→S=1μ0[λ2πε0aˆj×μ02πaλvˆi]
=λ2v4π2ε0a2(ˆj׈i)=−λ2v4π2ε0a2ˆk.

Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC WAVESExercise:NCERT Exemplar
Explore 7 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC WAVESExercise:Electromagnetic Spectrum
Explore 20 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC INDUCTIONExercise:Assertion And Reason
Explore 15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTIPSChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
An infinitely long time charge has linear charge density λC/m the line charge is along the line x=0,z=2m find the electric field at point (1,1,1) m.
View SolutionObtain the formula for the electric field due to a along thin wire of uniform linear charge density λ without using Gauss's law.
View Solution
Knowledge Check
An infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
A0.33×1011N/CB3×1011NC−1C0.66×1011NC−1D1.32×1011NC−1Twelve infinite long wire of uniform linear charge density (λ) are passing along the twelve edges of a cube. Find electric flux through any face of cube. ,
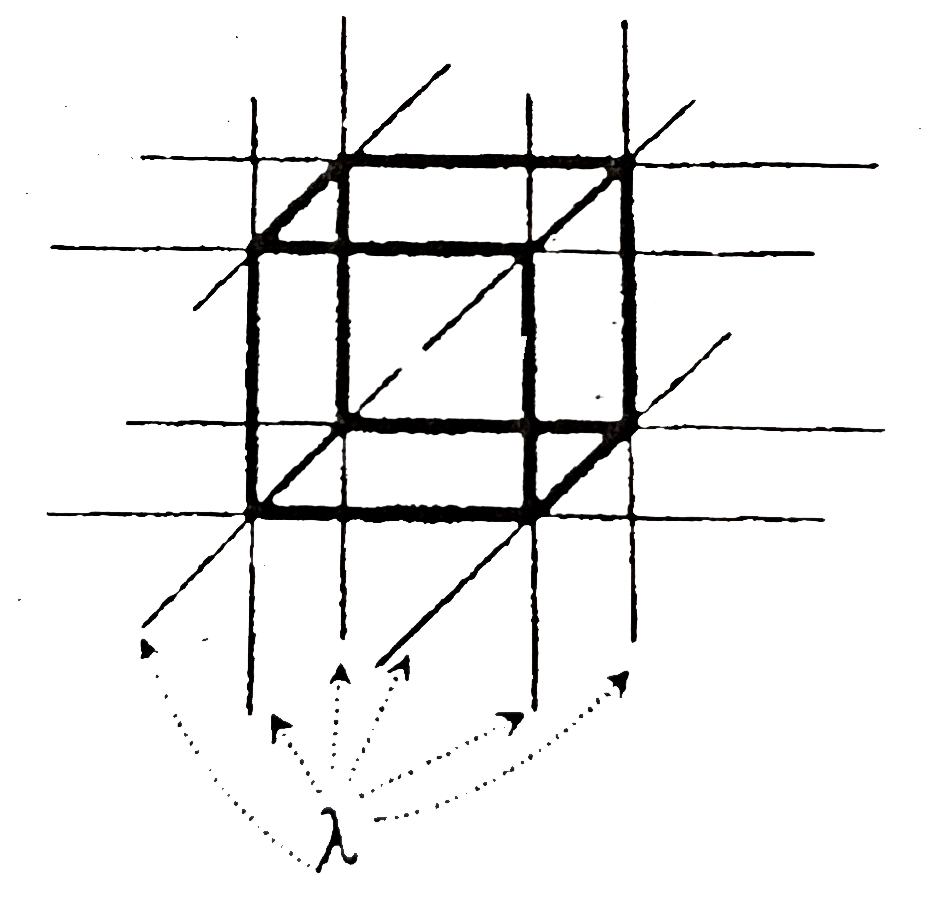 A(λl2ε0)B(λlε0)C(λl3ε0)D(3λlε0)
A(λl2ε0)B(λlε0)C(λl3ε0)D(3λlε0)Find ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
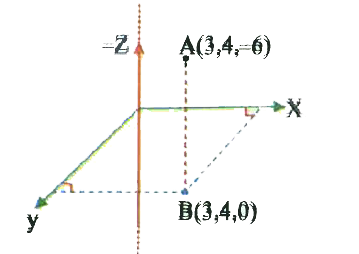 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1
An indinitely long positively charged wire has a linear charge density λcm−1. An electron is revolving around the wire as its center with a constant velocity in a circular plane perpendicular to the wire. Deduce the expression for KE of electron. Plot a graph of K.E as a function of charge density λ.
View SolutionTwo infinitely long thin styraight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
View SolutionTwo infinite length wires carries currents 8A and 6A respectively and placed along X and Y-axis. Magnetic field at a point P(0,0,d)m will be
View SolutionAn infinitely long wire carrying current I is along Y-axis such taht its one end is at point A(0,b) while the wire extends upto +∞. The magnitude of magnetic field strength at point (a,0) is

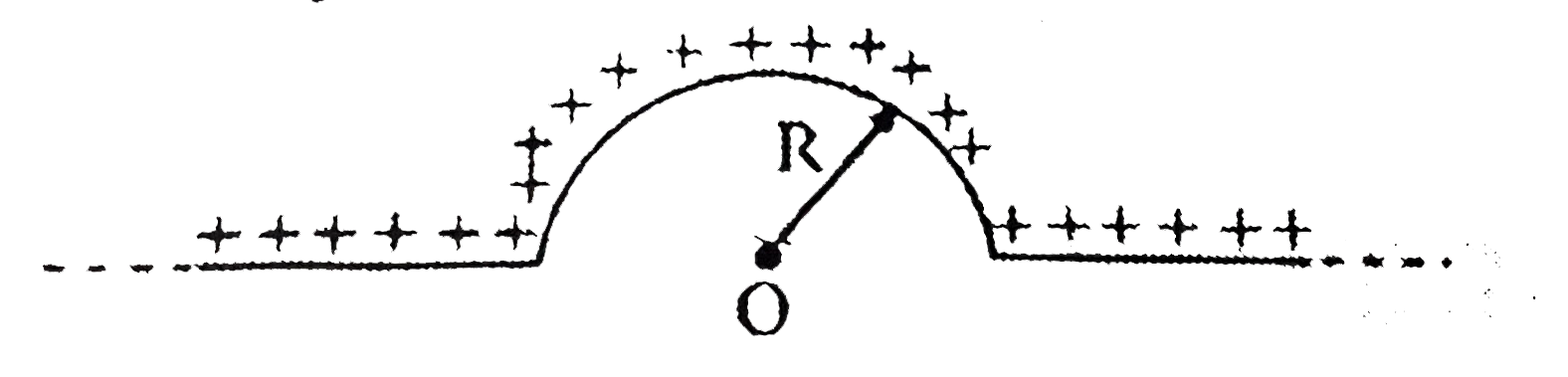
View SolutionThe electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
View Solution

