A particle of mass m is moving in YZ-plane with a uniform velocity v with its trajectory running parallel to +ve Y-axis and intersecting Z-axis at z=a in figure. The change in its angular momentum about the origin as it bounces elastically form a wall at y=constant is
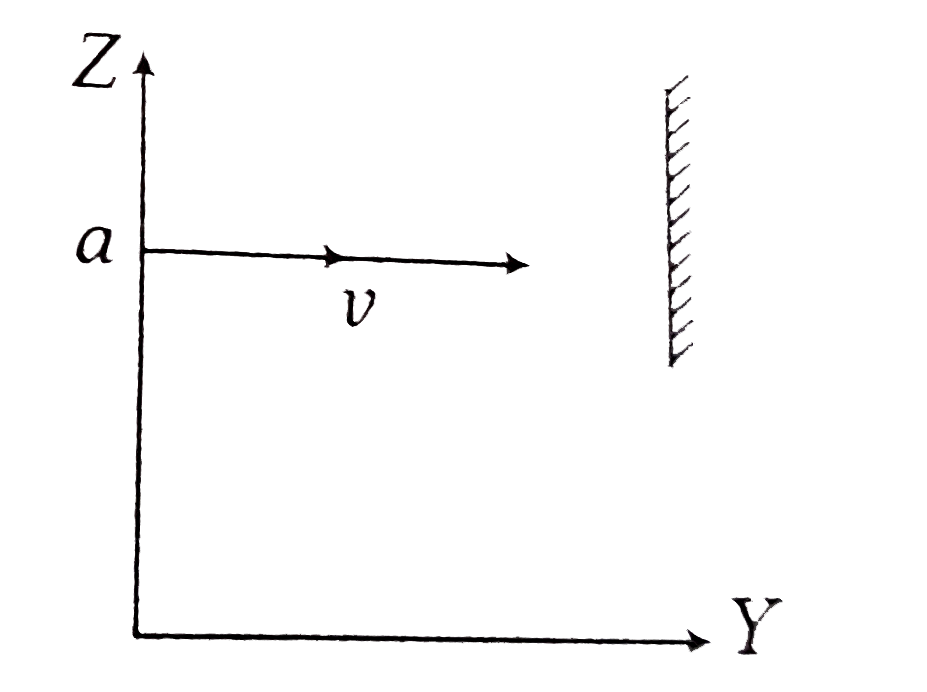
The initial velocity is
→vi=vˆey
After reflection from the wall, the final velocity is
→vf=−vˆey
The trajectory is given as
→r=yˆey+aˆez
Hence, the change in angular momentum is
Δ→L=→r×m(→vf−→vi)
=(yˆey+a→ez)×(−2mˆey)
=2mva→ex[∴ˆey׈ey=0 and ˆez׈ey=−ˆex]
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Assertion And Reason
15 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Higher Order Thinking Skills
8 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPERSEXERCISE - Practice Paper 3
50 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
A particle of mass m is moving in yz -plane with a uniform velocity v as shown in figure. It collides elastically with the wall AB. The change in its angular momentum about the origin as it bounces elastically from the wall is √α mvai . Find α.
'(##CEN_KSR_PHY_JEE_C09_E01_012_Q03##)'
View SolutionA particle is moving in the xy-plane with a constant velocity along a line parallel to the X-axis away from the origin. The magnitude of its angular momentum about the origin.
View Solution
Knowledge Check
A particle of mass m is moving in yz-plane with a unifrom velocity v with its trajectory running parallel to +ve y-axis and intersecting z-axis at z=a Fig. The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is :
 AmvaˆexB2mvaˆexCymvaˆexD2ymvaˆex
AmvaˆexB2mvaˆexCymvaˆexD2ymvaˆexA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
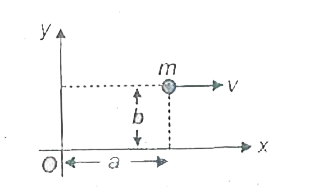 AmvbBmvaCmv√a2+b2Dmv(a+b)
AmvbBmvaCmv√a2+b2Dmv(a+b)A particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
Adecreases with timeBincreases with timeCremains constantDis zero
A particle of mass 0.75 kg is moving in the XY plane parallel to Y-axis, with a uniform speed of 4 m/s. It crosses the X-axis at 3 m from the origin. What is the angular momentum of the particle about the origin?
View SolutionA particle of mass m is moving on the XY-plane along a straight line y = d, with constant velocity v. Its angular momentum about the origin
View SolutionA particle of mass of m is moving along the side of square of side 'a' with a uniform speed u in the X-Y plane as shown in the figure.
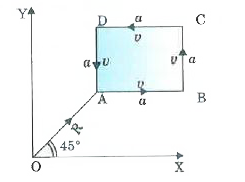
Which of the following statements is false for the angular momentum →L about the origin ?
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
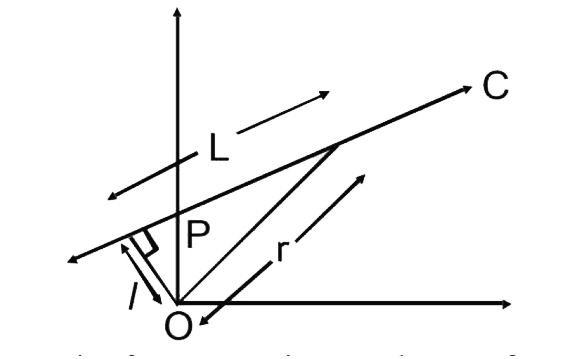
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
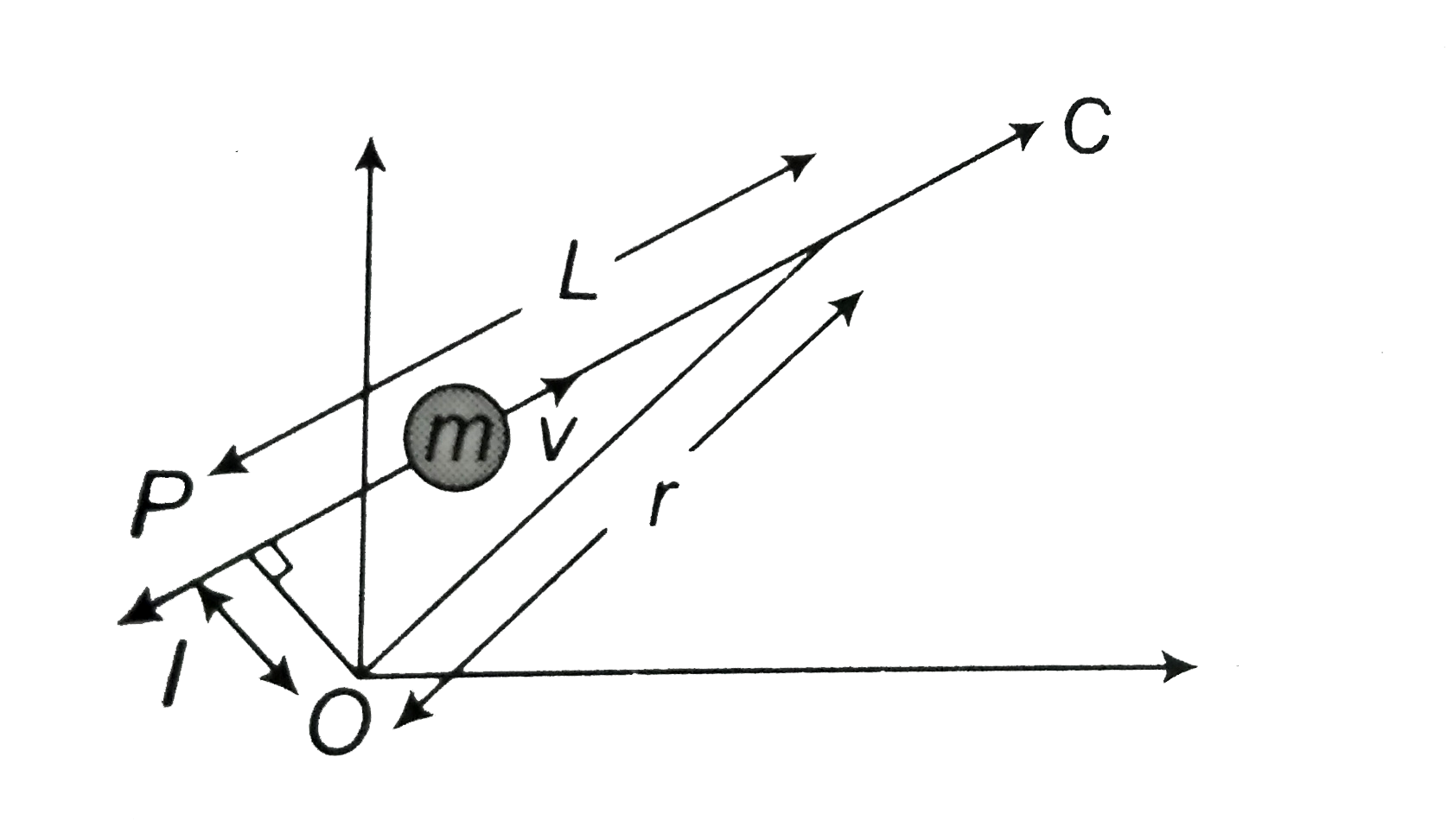
View Solution
