A disc is rotating with angular velocity ω. A force F acts at a point whose position vector with respect to the axis of rotation is r. The power associated with torque due to the force is given by
(→r×→F).→ω
(→r×→F)×→ω
→r.(→F×→ω)
→r×(→F.→ω)
The correct Answer is:a
Torque, →τ=→r×→F
∴ Power associated with the torque is
P=→τ.→ω=(→r×→F).→ω
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Equilibrium Of A Rigid Body
13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Moment Of Inertia
7 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Motion Of Centre Of Mass
10 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPERSEXERCISE - Practice Paper 3
50 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
A disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View SolutionTwo discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
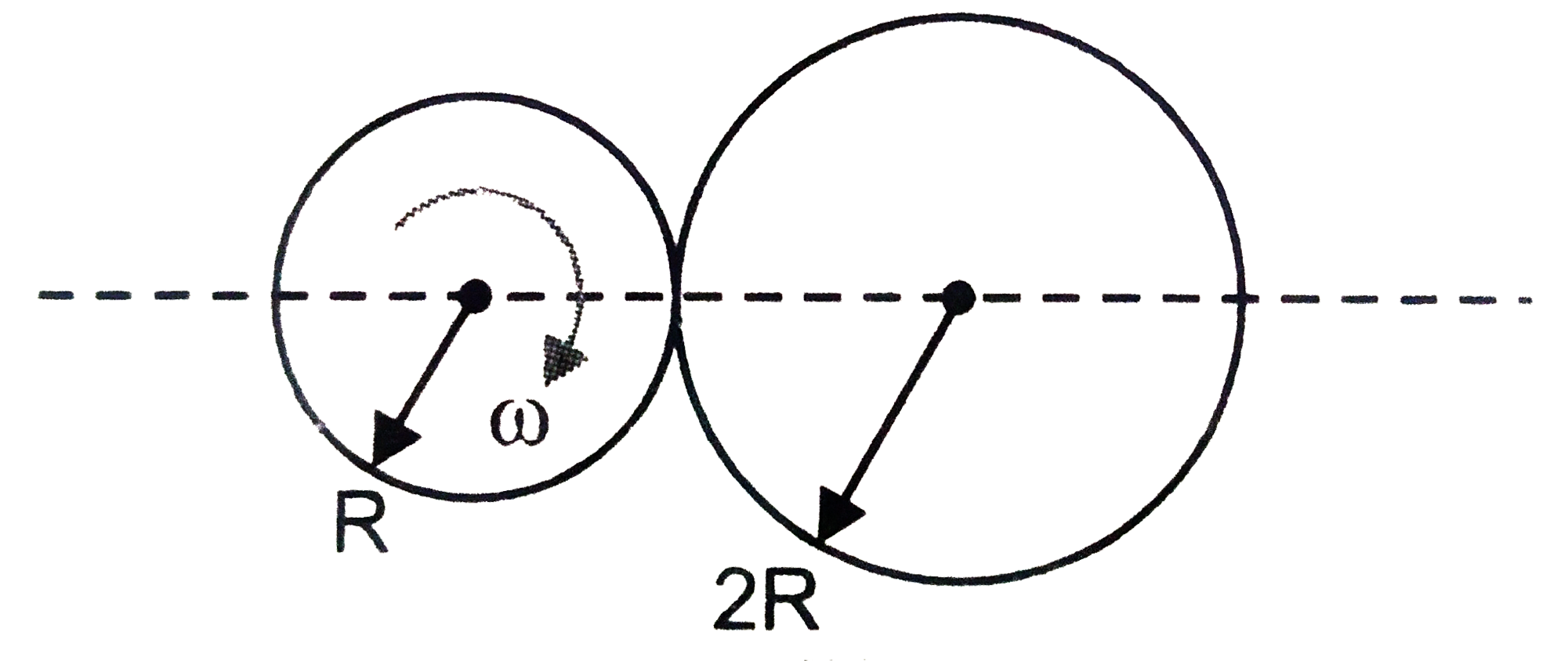
View Solution
Knowledge Check
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
ALinear momentumBAngular momentumCkinetic energyDMoment of inertiaA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A disc rotates with angular velocity ω and kinetic energy E. Then its angular momentum
AIωBL=EωCL=2EωDL=ωE
Let a force F be acting on a body free to rotate about a point O and let r be the position vector of any point P on the line of action of the force. Then torque (τ) of this force about point O is defined as τ=r×F Given, F=(2ˆi+3ˆj−ˆk)Nandr=(ˆi−ˆj+6ˆk)m. Find the torque of this force.
View SolutionA heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
View SolutionFind the torque about the origin when a force of 3ˆj N acts on a particle whose position vector is 2ˆk m
View SolutionA force →F=4ˆi−10ˆj acts on a body at a point having position vector −5ˆi−3ˆj relative to origin of co-ordinates on the axis of rotation. The torque acting on the body is
View SolutionDuring rotation of a body, the position vector is along X-axis and force vector is along Y-axis, The direction of torque vector is
View Solution