In the figure, is perpendicular to the chord of a circle whose centre is If is a diameter, show that
Since, (given) and the perpendicular drawn from the centre to a chord bisects the chord.
D is the mid -point of AB.
Also, O is the mid -point of BC.
Now, in , D and O are mid-points of AB and BC respectively.
Therefore, and .
or CA =2OD (mid-point theorem).
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD
View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn a circle OD is perpendicular to chord AB of a circle with centre O. If BC is a diameter then the AC/OD is:
View SolutionIn Figure, OA and OB ar respectively perpendiculars to chords CD and EF of a circle whose centre is O. If OA=OB , prove that CE=DF.
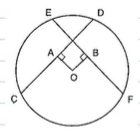
View SolutionIn the given figure, O is the centre of the circle.

Name all chords of the circle.
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionIn the given figure, AOB is a diameter of a circle with centre O. Find tan A tan B.
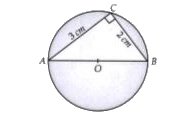
View SolutionIn given figure, O is the centre of the circle.
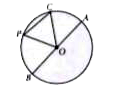
A chord, which is not the diameter of the circle is
View SolutionIn figure PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB=30∘, find ∠PCA
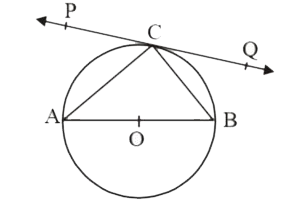
View Solution
