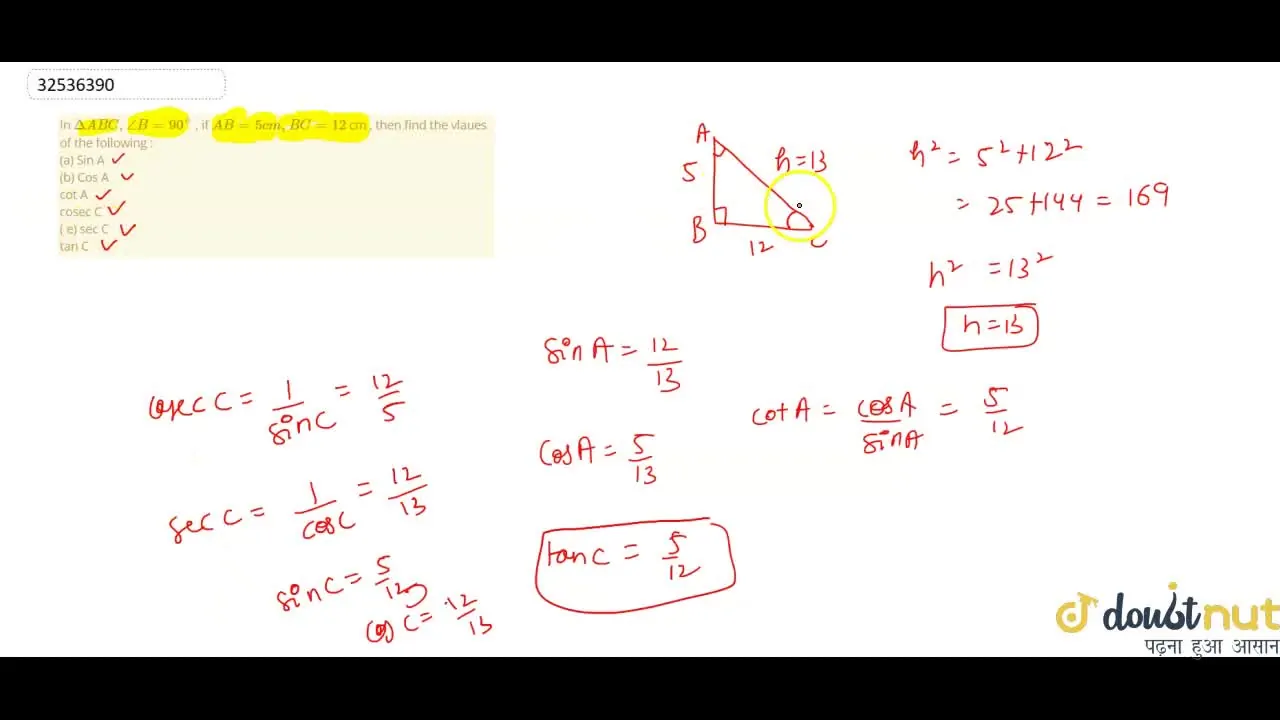
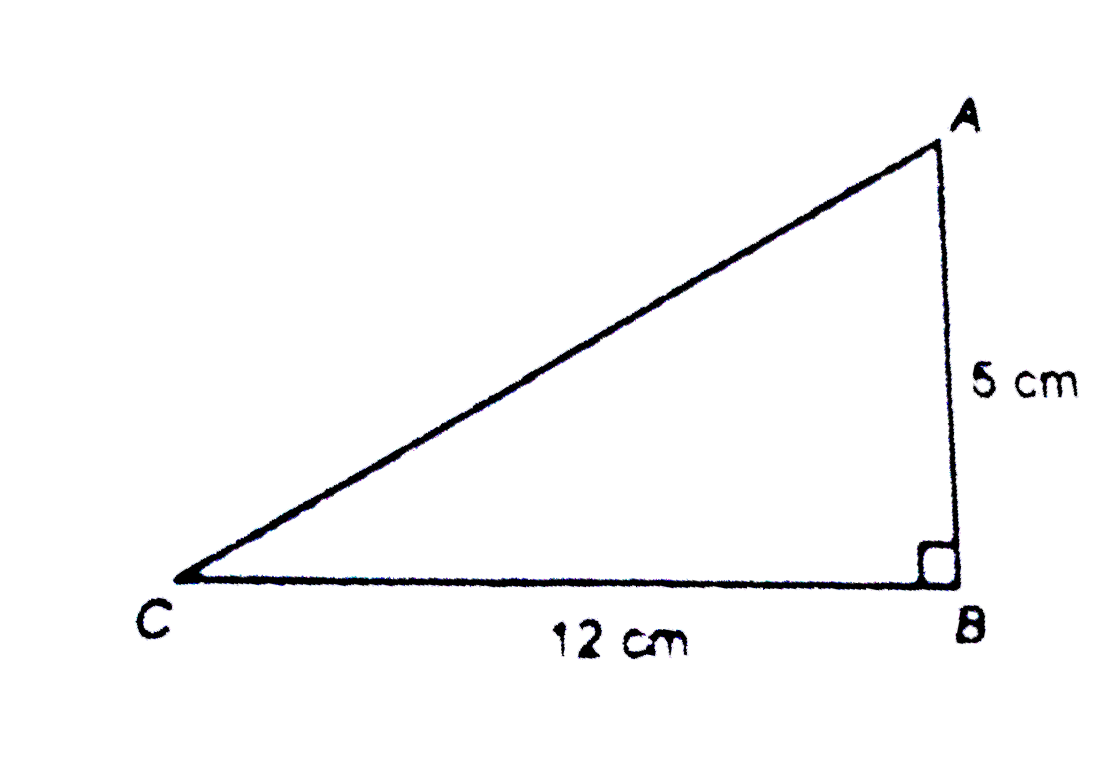
In , if cm , then find the vlaues of the following :
(a) Sin A
(b) Cos A
cot A
cosec C
( e) sec C
tan C
In , from Pythagoras theorem
cm
For A, base is AB , perpendicular is BC.
For base is BC , perpendicular is AB,
while hypotenuse is same i.e., AC for both the angles
(a)
(b)
(c )
(d)
(e )
(f)
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Problems From NCERT/exemplar29videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a20videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - PROBLEMS FROM NCERT/ EXEMPLAR10videos
CONSTRUCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions8videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
In ΔABC,∠B=90∘,AB=24cmandAC=26cm then find the values of the following :
(i) tanA
(ii) cot C
(iii) cosC
(iv) sinC
(v) cosecA
(vi) sec AView SolutionInΔABC,∠A=0=90∘,AB=6cmandAC=8cm, then find the values of the following :
(i) sinB
(ii)sinA
(iii) tanB
(iv)secB
(v)cotC
(vi) "cosec" CView SolutionIn a ΔABC,∠B=90∘,AB=7cmand(AC−BC)=1cm, find the values of sinA,cosA,sinCandC.
View SolutionIf in ΔABC,∠B=90∘,AB=6√3 and AC=12cm, find BC.
View SolutionIn ΔABC,∠C=90∘andAB=c,BC=a,CA=b , then the value of cosec B-cos A) is
View SolutionIn ΔABC,∠B=90∘,∠A=30∘,b=20cm, find a and c.
View SolutionIn a ΔABC,∠B=90∘,AB=5cmand(BC+AC)=25cm. Find the values of sinA,cosA,cosec AandsecA.
View SolutionIn ΔABC,∠C=90∘andAB=c,BC=a,CA=b , then the value of cosec B-cos A) is
View SolutionIn ΔABC,right -angled at B,AB=5cmandBC=12cm. find the values of sinA,secA,sinCandsecC.
View SolutionIn ΔABC,∠B is right angle, AB = 5 cm and BC = 12cm , then the value of cosC is :
View Solution