Suppose that 6% of the people with blood group O are left handed and 10% of those with other blood groups are left handed, 30 % of the people have blood groups O. If a left handed person os selected at random, what is the probability that he/she will have blood group O?
To solve the problem, we will use Bayes' theorem to find the probability that a randomly selected left-handed person has blood group O.
1. Define Events:
- Let E1: the event that a person has blood group O.
- Let E2: the event that a person has some other blood group.
- Let E3: the event that a person is left-handed.
2. Given Information:
- P(E1)=0.30 (30% of people have blood group O)
- P(E2)=0.70 (70% of people have other blood groups, since P(E2)=1−P(E1))
- P(E3|E1)=0.06 (6% of people with blood group O are left-handed)
- P(E3|E2)=0.10 (10% of people with other blood groups are left-handed)
3. Find P(E3):
Using the law of total probability:
P(E3)=P(E3|E1)⋅P(E1)+P(E3|E2)⋅P(E2)
Substituting the values:
P(E3)=(0.06⋅0.30)+(0.10⋅0.70)
P(E3)=0.018+0.07=0.088
4. Apply Bayes' Theorem:
We want to find P(E1|E3):
P(E1|E3)=P(E3|E1)⋅P(E1)P(E3)
Substituting the known values:
P(E1|E3)=0.06⋅0.300.088
P(E1|E3)=0.0180.088
P(E1|E3)=1888=944
5. Final Answer:
The probability that a randomly selected left-handed person has blood group O is 944.
- Let E1: the event that a person has blood group O.
- Let E2: the event that a person has some other blood group.
- Let E3: the event that a person is left-handed.
- P(E1)=0.30 (30% of people have blood group O)
- P(E2)=0.70 (70% of people have other blood groups, since P(E2)=1−P(E1))
- P(E3|E1)=0.06 (6% of people with blood group O are left-handed)
- P(E3|E2)=0.10 (10% of people with other blood groups are left-handed)
Using the law of total probability:
P(E3)=P(E3|E1)⋅P(E1)+P(E3|E2)⋅P(E2)
Substituting the values:
P(E3)=(0.06⋅0.30)+(0.10⋅0.70)
P(E3)=0.018+0.07=0.088
We want to find P(E1|E3):
P(E1|E3)=P(E3|E1)⋅P(E1)P(E3)
Substituting the known values:
P(E1|E3)=0.06⋅0.300.088
P(E1|E3)=0.0180.088
P(E1|E3)=1888=944
The probability that a randomly selected left-handed person has blood group O is 944.
Topper's Solved these Questions
Similar Questions
Knowledge Check
People of AB blood group have :
Aantigen 'B' and antibodies 'a'Bantibodies 'a' and 'b',but no antigensCantigens 'A' and 'B' but no antibodiesDantigens 'A' and 'B' and their antibodiesWhat is correct for a person with blood group 'O' ?
AThe person has no antigen 'A'and 'B' antibodies on his RBCs.BHis blood plasma has antibodies for both 'A' and 'B' antigensCBoth (a) and (b)DNone of theseIf blood group of parents are AB and O, the possible bloodd groups of children are:
AA or B groupBO+ group onlyCO− group onlyDAB group only
Blood groups of a couple are AB and O. the possible blood groups of children would be
View SolutionIn a medical examination of students of a class, the following blood groups are recoreded.
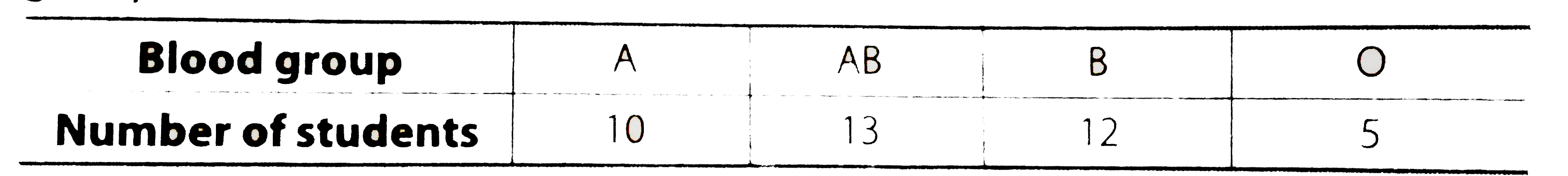
A student is selected at random from the class. The probability that he/she has blod group B, is
View SolutionThe probality of a having a child with blood group O to parents with blood groups A and B is
View SolutionThe possible blood group of the offspring of the prents with blood group 'O' and 'AB':
View SolutionA women with blood group 'O' has a child with blood group 'O'. Father with blood group 'A' must have the genotype
View Solution
